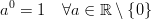Why is Math.pow(0, 0) === 1?

Question

We all know that 0⁰ is indeterminate.

But, javascript says that:

Math.pow(0, 0) === 1 // true

and C++ says the same thing:

pow(0, 0) == 1 // true

WHY?

I know that:

>Math.pow(0.001, 0.001)
0.9931160484209338

But why does Math.pow(0, 0) throw no errors? Or maybe a NaN would be better than 1.

@zzzzBov: Under the standard definition, "a^b = exp(b ln(a))", it's undefined. Trying to define it as "limit_x->0 f(x)^g(x)" where "f" and "g" both have limits of zero gives an indeterminate value, since it depends on your choice of functions. (Apologies for the mangled notation; I can't figure out how to get superscripts in comments). — Mike Seymour, Nov 13 '13 at 14:30
@MikeSeymour, yes, I'm aware that 0⁰ (use unicode characters) is undefined given that definition, however, if you read my comment you should note that the quotation references the "world of mathematics" rather than any "standard definition". It's this difference that I was originally referring, and the question has been updated to correct this nuance. — zzzzBov, Nov 13 '13 at 14:34
It allows functions that depend upon products of probabilities to deliver sensible results. It's an incorrect notion that computers are symbolic math processors. The C language has a specific implementation in the real world while your mathematical world might be too ideal to be inplemented in silicon. — IRTFM, Nov 13 '13 at 21:54
For the mathematical version of this question — “why do we often define 0^0 = 1?” — math.stackexchange has lots of good answers: http://math.stackexchange.com/questions/11150/zero-to-the-zero-power-is-00-1 — PLL, Nov 13 '13 at 22:03
IMHO 0^0 *should* be NaN, just as 0/0 is for floating point, because the limit is not uniquely defined. In contrast, 1/0 IS well-defined as Infinity. Anyone who argues that 0^0 should be 1 because x^0=1 for non-zero x is only looking at half of it - don't forget that 0^y=0 for y>0. I think the real answer to this question is "because CS majors are no longer math majors like they were in the 1940's." — Matt, Nov 14 '13 at 01:47

Shafik Yaghmour · Accepted Answer · 2013-11-13T18:42:51.443

In C++ ~~The result of pow(0, 0)~~ the result is basically implementation defined behavior since mathematically we have a contradictory situation where N^0 should always be 1 but 0^N should always be 0 for N > 0, so you should have no expectations mathematically as to the result of this either. This Wolfram Alpha forum posts goes into a bit more details.

Although having pow(0,0) result in 1 is useful for many applications as the Rationale for International Standard—Programming Languages—C states in the section covering IEC 60559 floating-point arithmetic support:

Generally, C99 eschews a NaN result where a numerical value is useful. [...] The results of pow(∞,0) and pow(0,0) are both 1, because there are applications that can exploit this definition. For example, if x(p) and y(p) are any analytic functions that become zero at p = a, then pow(x,y), which equals exp(y*log(x)), approaches 1 as p approaches a.

Update C++

As leemes correctly pointed out I originally linked to the reference for the complex version of pow while the non-complex version claims it is domain error the draft C++ standard falls back to the draft C standard and both C99 and C11 in section 7.12.7.4 The pow functions paragraph 2 says (emphasis mine):

[...]A domain error may occur if x is zero and y is zero.[...]

which as far as I can tell means this behavior is unspecified behavior Winding back a bit section 7.12.1 Treatment of error conditions says:

[...]a domain error occurs if an input argument is outside the domain over which the mathematical function is defined.[...] On a domain error, the function returns an implementation-defined value; if the integer expression math_errhandling & MATH_ERRNO is nonzero, the integer expression errno acquires the value EDOM; [...]

So if there was a domain error then this would be implementation defined behavior but in both the latest versions of gcc and clang the value of errno is 0 so it is not a domain error for those compilers.

Update Javascript

For Javascript the ECMAScript® Language Specification in section 15.8 The Math Object under 15.8.2.13 pow (x, y) says amongst other conditions that:

If y is +0, the result is 1, even if x is NaN.

@leemes I believe that page is wrong, the standard does not say that NaN should be returned. The return value is implementation-defined. cplusplus.com which you claim is not a reliable source is actually more accurate here. — interjay, Nov 13 '13 at 14:42
@interjay I guess you mean the deleted answer; I only quoted about its inreliability, hoping it could explain the downvote (which was not by me). Well, both pages are wikis, so their reliability depends on their editors which are human and make mistakes. ;) — leemes, Nov 13 '13 at 14:53
@leemes the C++ community on SO [definitely has a strong dislike for cplusplus.com](http://meta.stackexchange.com/questions/194788/links-being-changed-to-cppreference-com) — Shafik Yaghmour, Nov 13 '13 at 14:57
@ShafikYaghmour I linked the same question (in the deleted answer). — leemes, Nov 13 '13 at 16:03
@Shafik: Excellent answer; to the point (by citing the authoritative source) but also informative (by citing the rationale). — alecov, Nov 13 '13 at 22:43
@Alek I appreciate the feedback, I try to write the answers I would like to read from others. I don't always succeed but I try. Writing good questions is even harder, I have only attempted that once and I spent way longer on it then I do on my answers. — Shafik Yaghmour, Nov 13 '13 at 22:55

score 35 · Answer 2 · answered Nov 13 '13 at 14:16

In JavaScript Math.pow is defined as follows:

If y is NaN, the result is NaN.

If y is +0, the result is 1, even if x is NaN.

If y is −0, the result is 1, even if x is NaN.

If x is NaN and y is nonzero, the result is NaN.

If abs(x)>1 and y is +∞, the result is +∞.

If abs(x)>1 and y is −∞, the result is +0.

If abs(x)==1 and y is +∞, the result is NaN.

If abs(x)==1 and y is −∞, the result is NaN.

If abs(x)<1 and y is +∞, the result is +0.

If abs(x)<1 and y is −∞, the result is +∞.

If x is +∞ and y>0, the result is +∞.

If x is +∞ and y<0, the result is +0.

If x is −∞ and y>0 and y is an odd integer, the result is −∞.

If x is −∞ and y>0 and y is not an odd integer, the result is +∞.

If x is −∞ and y<0 and y is an odd integer, the result is −0.

If x is −∞ and y<0 and y is not an odd integer, the result is +0.

If x is +0 and y>0, the result is +0.

If x is +0 and y<0, the result is +∞.

If x is −0 and y>0 and y is an odd integer, the result is −0.

If x is −0 and y>0 and y is not an odd integer, the result is +0.

If x is −0 and y<0 and y is an odd integer, the result is −∞.

If x is −0 and y<0 and y is not an odd integer, the result is +∞.

If x<0 and x is finite and y is finite and y is not an integer, the result is NaN.

_{emphasis mine}

as a general rule, native functions to any language should work as described in the language specification. Sometimes this includes explicitly "undefined behavior" where it's up to the implementer to determine what the result should be, however this is not a case of undefined behavior.

Annex F in the C99 and C11 standards contains this same specification. An implementation is supposed to define `__STDC_IEC_559__` to announce that it conforms to this specification. Annex F describes IEC 60559 floating-point arithmetic. I believe a C specification is allowed to partially conform to Annex F (e.g. pow(0, 0) == 1) and not define `__STDC_IEC_559__`. — Howard Hinnant, Nov 13 '13 at 16:50
@HowardHinnant hmmm, it seems that in the case of [gcc](https://groups.google.com/forum/#!topic/gnu.gcc.help/P4vx6fnqDGg) and [clang](https://sourceware.org/bugzilla/show_bug.cgi?id=6981) that piece of information may not be totally helpful, that is discouraging. — Shafik Yaghmour, Nov 13 '13 at 18:05
I don't know that this answer helps. Of course the function should perform as it is defined in the spec. But then the question just becomes "Why was it defined this way in the spec?" — Beska, Nov 13 '13 at 18:28
Good thing this is (probably) done in hardware, else it would nuke performance with all these special cases :) — Thomas, Nov 13 '13 at 21:58

schmijos · Answer 3 · 2013-11-14T09:17:04.280

17

It is just convention to define it as 1, 0 or to leave it undefined. The definition pow(0,0) is wide spread because of the following definition:

mathematical power definition

ECMA-Script documentation says the following about pow(x,y):

If y is +0, the result is 1, even if x is NaN.

If y is −0, the result is 1, even if x is NaN.

[ http://www.ecma-international.org/ecma-262/5.1/#sec-15.8.2.13 ]

edited Nov 14 '13 at 09:17

answered Nov 13 '13 at 14:29

schmijos

8,114
3
50
58

3

math.stackexchange has lots of good discussion and explanations for the definition 0^0=1: http://math.stackexchange.com/questions/11150/zero-to-the-zero-power-is-00-1 – PLL Nov 13 '13 at 22:04

score 14 · Answer 4 · answered Nov 13 '13 at 14:30

According to Wikipedia:

In most settings not involving continuity in the exponent, interpreting 0⁰ as 1 simplifies formulas and eliminates the need for special cases in theorems.

There are several possible ways to treat 0**0 with pros and cons to each (see Wikipedia for an extended discussion).

The IEEE 754-2008 floating point standard recommends three different functions:

pow treats 0**0 as 1. This is the oldest defined version. If the power is an exact integer the result is the same as for pown, otherwise the result is as for powr (except for some exceptional cases).
pown treats 0**0 as 1. The power must be an exact integer. The value is defined for negative bases; e.g., pown(−3,5) is −243.
powr treats 0**0 as NaN (Not-a-Number – undefined). The value is also NaN for cases like powr(−3,2) where the base is less than zero. The value is defined by exp(power'×log(base)).

score 7 · Answer 5 · edited Nov 09 '22 at 19:30

Donald Knuth

sort of settled this debate in 1992 with the following:

enter image description here

And went even more into details in his paper Two Notes on Notation.

Basically, while we don't have 1 as the limit of f(x)/g(x) for all not all functions f(x) and g(x), it still makes combinatorics so much simpler to define 0^0=1, and then just make special cases in the few places where you need to consider functions such as 0^x, which are weird anyway. After all x^0 comes up a lot more often.

Some of the best discussions I know of this topic (other than the Knuth paper) are:

If you have not read some read the answers in [Zero to the zero power...?](http://math.stackexchange.com/questions/11150/zero-to-the-zero-power-is-00-1) which was linked off the question you should some of the answers covers this approach as well. — Shafik Yaghmour, Dec 06 '13 at 18:02

score 5 · Answer 6 · answered Nov 13 '13 at 14:17

When you want to know what value you should give to f(a) when f isn't directly computable in a, you compute the limit of f when x tends towards a.

In case of x^y, usual limits tend towards 1 when x and y tend to 0, and especially x^x tends towards 1 when x tends to 0.

See http://www.math.hmc.edu/funfacts/ffiles/10005.3-5.shtml

score 5 · Answer 7 · answered Nov 13 '13 at 14:26

The C language definition says (7.12.7.4/2):

A domain error may occur if x is zero and y is zero.

It also says (7.12.1/2):

On a domain error, the function returns an implementation-defined value; if the integer expression math_errhandling & MATH_ERRNO is nonzero, the integer expression errno acquires the value EDOM; if the integer expression math_errhandling & MATH_ERREXCEPT is nonzero, the ‘‘invalid’’ floating-point exception is raised.

By default, the value of math_errhandling is MATH_ERRNO, so check errno for the value EDOM.

Whoups! That's really interesting! I compiled my cpp file using `g++ (Ubuntu/Linaro 4.8.1-10ubuntu8) 4.8.` — Ionică Bizău, Nov 13 '13 at 14:27

NiloCK · Answer 8 · 2013-12-06T19:02:01.823

I'd like to disagree with some of the previous answers' assertion that it's a matter of convention or convenience (covering some special cases for various theorems, etc) that 0^0 be defined as 1 instead of 0.

Exponentiation doesn't actually fit that well with our other mathematical notations, so the definition we all learn leaves room for confusion. A slightly different way of approaching it is to say that a^b (or exp(a, b), if you like) returns the value multiplicatively equivalent to multiplying some other thing by a, repeated b times.

When we multiply 5 by 4, 2 times, we get 80. We've multiplied 5 by 16. So 4^2 = 16.

When you multiply 14 by 0, 0 times, we are left with 14. We've multiplied it 1. Hence, 0^0 = 1.

This line of thinking might also help to clarify negative and fractional exponents. 4^(-2) is a 16th, because 'negative multiplication' is division - we divide by four twice.

a^(1/2) is root(a), because multiplying something by the root of a is half the multiplicative work as multiplying it by a itself - you would have to do it twice to multiply something by 4 = 4^1 = (4^(1/2))^2

This is still conventional. And the convenience reasons for application in the program languages are well-documented in several specifications, so the reason to take alternative definitions is quite weak, despite your disagreement. — FrankHB, Nov 27 '21 at 08:49

score 0 · Answer 9 · answered Nov 03 '15 at 16:26

For this to understand you need to solve calculus:

Expanding x^x around zero using Taylor series, we get:

So to understand what's going on with limit when x goes to zero, we need to find out what's going on with second term x log(x), because other terms are proportional to x log(x) raised to some power.

We need to use transformation:

Now after this transformation we can use L'Hôpital's rule, which states that:

So differentiating that transformation we get:

So we've calculated that term log(x)*x approaches 0 when x approaches 0. It's easy to see that other consecutive terms also approaches zero and even faster than second term.

So at point x=0, series becomes 1 + 0 + 0 + 0 + ... and thus equals to 1.

While this answer is impressive, it's worth noting that in math, the limit as x->a of f(x) doesn't necessarily equal f(a), unless the function is continuous at x. — , Apr 23 '17 at 04:48

Why is Math.pow(0, 0) === 1?

9 Answers9

Donald Knuth

Linked