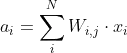125

I am trying to build a neural network from scratch. Across all AI literature there is a consensus that weights should be initialized to random numbers in order for the network to converge faster.

But why are neural networks initial weights initialized as random numbers?

I had read somewhere that this is done to "break the symmetry" and this makes the neural network learn faster. How does breaking the symmetry make it learn faster?

Wouldn't initializing the weights to 0 be a better idea? That way the weights would be able to find their values (whether positive or negative) faster?

Is there some other underlying philosophy behind randomizing the weights apart from hoping that they would be near their optimum values when initialized?

kmario23
  • 57,311
  • 13
  • 161
  • 150
Shayan RC
  • 3,152
  • 5
  • 33
  • 40

8 Answers8

157

Breaking symmetry is essential here, and not for the reason of performance. Imagine first 2 layers of multilayer perceptron (input and hidden layers):

enter image description here

During forward propagation each unit in hidden layer gets signal:

enter image description here

That is, each hidden unit gets sum of inputs multiplied by the corresponding weight.

Now imagine that you initialize all weights to the same value (e.g. zero or one). In this case, each hidden unit will get exactly the same signal. E.g. if all weights are initialized to 1, each unit gets signal equal to sum of inputs (and outputs sigmoid(sum(inputs))). If all weights are zeros, which is even worse, every hidden unit will get zero signal. No matter what was the input - if all weights are the same, all units in hidden layer will be the same too.

This is the main issue with symmetry and reason why you should initialize weights randomly (or, at least, with different values). Note, that this issue affects all architectures that use each-to-each connections.

Community
  • 1
  • 1
ffriend
  • 27,562
  • 13
  • 91
  • 132
  • 1
    Great explaination. But why use the word `symmetry` not `correlation`? Who used the word first? – nn0p Apr 01 '16 at 14:46
  • 2
    @nn0p: correlation implies that 2 signals change in a similar direction, but not always and not with exactly the same magnitude. At least as far as I know, symmetry doesn't have formal definition and is used here to represent _exactly_ the same signals over all links between nodes, which makes training useless. – ffriend Apr 01 '16 at 23:45
  • @ffriend than in case we use dropout, the randomization is not more needed. Am I wrong? – emanuele Jun 28 '16 at 23:53
  • 4
    @emanuele Dropout is itself a kind of randomization, so yes, it should work. Yet, all connections that are not "dropped out" at each iteration, will still get symmetric update, so I guess learning will be quite slow and thus recommend to still use random initialization in any practical network. – ffriend Jul 01 '16 at 23:20
  • This explains forwardprop well, but what about backprop? – zell May 01 '20 at 12:41
  • @zell backward pass is more tricky: for layers from second to last gradients stay the same since both - forward and backward signals (e.g. activations from earlier layers and gradients from later ones) - are the same. In the first layer, however, weights may differ since inputs are different (at least for linear layer gradient of weights is a function of gradient from later layer and _inputs_ which are different). After first update weights of the first layer will get different weights and so symmetry at _that_ layer will be broken. – ffriend May 02 '20 at 16:05
  • I _think_ symmetry will get broken one layer at a time, so in a network with N layers first N updates will be spent on something that could have been done using random initialization. Also I said that gradients _may_ differ because I can't say it for sure for all possible layers. Maybe yes, maybe no, I never did such an analysis. In any case, initializing weights with random values (normally distributed or something smarter like Xavier initialization) helps to avoid all kinds of pitfalls. – ffriend May 02 '20 at 16:16
  • @ffriend Breaking symmetry happens only for the weights connecting the input and hidden layer. This means that neurons are still different in the hidden layer. – ado sar Apr 10 '22 at 14:28
90

Analogy:

Imagine that someone has dropped you from a helicopter to an unknown mountain top, and you're trapped there. Fog everywhere. You only know that you should get down to the sea level somehow. Which direction should you take to get down to the lowest possible point?

If you couldn't reach sea level, the helicopter would take you again and drop you at the same mountain top. You would have to take the same directions again because you're "initializing" yourself to the same starting positions.

However, each time the helicopter drops you somewhere randomly on the mountain, you would take different directions and steps. So, you would have a better chance of reaching the lowest possible point.

That is what is meant by breaking the symmetry. The initialization is asymmetric (which is different), so you can find different solutions to the same problem.

In this analogy, where you land is the weight. So, with different weights, there's a better chance of reaching the lowest (or lower) point.

Also, it increases the entropy in the system so the system can create more information to help you find the lower points (local or global minimums).

enter image description here

Inanc Gumus
  • 25,195
  • 9
  • 85
  • 101
  • 20
    It seems that the helicopter drop you somewhere random on the mountain several times, however in deep learning we just initial the weights randomly only one time. – YuFeng Shen Oct 24 '17 at 09:04
  • 1
    This is a real intuitive explanation. We should also note NNs are almost never convex - so the randomization is ideal way to go - but if you have a convex loss function, then of course it does not matter what you initialize your weights to. – Kingz May 18 '18 at 19:05
  • 12
    It's a good analogy - but it makes more sense to assume that you and your friends are being dropped on the mountain (i.e. nodes in a network) - either in the same spot or different people at different spots. And assume you could all communicate with each other. Different spots with communication will allow a faster descent. Same spot means everyone is likely to take the same path down. – ahmedhosny Jul 25 '18 at 20:40
26

The answer is pretty simple. The basic training algorithms are greedy in nature - they do not find the global optimum, but rather - "nearest" local solution. As the result, starting from any fixed initialization biases your solution towards some one particular set of weights. If you do it randomly (and possibly many times) then there is much less probable that you will get stuck in some weird part of the error surface.

The same argument applies to other algorithms, which are not able to find a global optimum (k-means, EM, etc.) and does not apply to the global optimization techniques (like SMO algorithm for SVM).

lejlot
  • 64,777
  • 8
  • 131
  • 164
  • So, it is not guaranteed that it will not get stuck in local minima just by randomizing? But after multiple runs with different randomized weights it might get the global minimum? – Shayan RC Nov 18 '13 at 03:57
  • 1
    There is no guarantee, but multiple initializations can help at least get near the true optimum. – lejlot Nov 18 '13 at 07:35
  • Is there any standard formula or rule to set value to initialize the weights?? I have feed-forward, multi-layer, back-propagation neural network, where sigmoid function is used. – lkkkk Oct 30 '14 at 05:54
  • there are some rule of the thumb in the S.Haykin book "neural networks" – lejlot Oct 30 '14 at 07:33
  • 5
    This is not the reason why people use random initialization as most people don't restart the training many times with different random initializations and the net is still able to get to a good local optima. – cesarsalgado Dec 09 '15 at 23:11
  • As @cesarsalgado said, this is NOT the (primary) reason weights are initialized randomly!! Weights are initialized randomly so that the neurons in a layer learn different aspects of the input, and thus the whole network is able to learn better. – A_C Jan 04 '22 at 17:32
6

As you mentioned, the key point is breaking the symmetry. Because if you initialize all weights to zero then all of the hidden neurons(units) in your neural network will be doing the exact same calculations. This is not something we desire because we want different hidden units to compute different functions. However, this is not possible if you initialize all to the same value.

Safak Ozdek
  • 906
  • 11
  • 18
2

Let be more mathematical. In fact, the reason I answer is that I found this bit lacking in the other answers. Assume you have 2 layers. If we look at the back-propagation algorithm, the computation of

dZ2 = A2 - Y

dW2 = (1/m) * dZ2 * A2.T

Let's ignore db2. (Sorry not sorry ;) )

dZ1 = W2.T * dZ2 .* g1'(Z1)

...

The problem you see is in bold. Computing dZ1 (which is required to compute dW1) has W2 in it which is 0. We never got a chance to change the weights to anything beyond 0 and we never will. So essentially, the neural network does not learn anything. I think it is worse than logistic regression (single unit). In the case of logistic regression, you learn with more iterations since you get different input thanks to X. In this case, the other layers are always giving the same output so you don't learn at all.

Muhammad Mubashirullah Durrani
  • 329
  • 3
  • 16
2

I learned one thing: if you initialize the weight to zeros, it's obvious that the activation units in the same layer will be the same, that means they'll have the same values. When you backbrop, you will find that all the rows of the gradient dW are the same also, hence all the rows of the weight matrix W are the same after gradient descent updates. In general, initializing all the weights to zero results in the network failing to break symmetry. This means that every neuron in each layer will learn the same thing, and you might as well be training a neural network with n[l]=1n[l]=1 for every layer, and the network is no more powerful than a linear classifier such as logistic regression. Andrew Ng course:

abdoulsn
  • 842
  • 2
  • 16
  • 32
1

In addition to initialization with random values, initial weights should not start with large values. This is because we often use the tanh and sigmoid functions in hidden layers and output layers. If you look at the graphs of the two functions, after forward propagation at the first iteration results in higher values, and these values correspond to the places in the sigmoid and tanh functions that converge the derivative to zero. This leads to a cold start of the learning process and an increase in learning time. As a result, if you start weights at random, you can avoid these problems by multiplying these values by values such as "0.01" or "0.001".

mustafamuratcoskun
  • 36
  • 5
1

First of all, some algorithms converge even with zero initial weightings. A simple example is a Linear Perceptron Network. Of course, many learning networks require random initial weighting (although this is not a guarantee of getting the fastest and best answer).

Neural networks use Back-propagation to learn and to update weights, and the problem is that in this method, weights converge to the local optimal (local minimum cost/loss), not the global optimal.

Random weighting helps the network to take chances for each direction in the available space and gradually improve them to arrive at a better answer and not be limited to one direction or answer.

[The image below shows a one-dimensional example of how convergence. Given the initial location, local optimization is achieved but not a global optimization. At higher dimensions, random weighting can increase the chances of being in the right place or starting better, resulting in converging weights to better values.][1]

[1]: https://i.stack.imgur.com/2dioT.png [Kalhor, A. (2020). Classification and Regression NNs. Lecture.]

In the simplest case, the new weight is as follows:

W_new = W_old + D_loss

Here the cost function gradient is added to the previous weight to get a new weight. If all the previous weights are the same, then in the next step all the weights may be equal. As a result, in this case, from a geometric point of view, the neural network is inclined in one direction and all weights are the same. But if the weights are different, it is possible to update the weights by different amounts. (depending on the impact factor that each weight has on the result, it affects the cost and the updates of the weights. So even a small error in the initial random weighting can be solved).

This was a very simple example, but it shows the effect of random weighting initialization on learning. This enables the neural network to go to different spaces instead of going to one side. As a result, in the process of learning, go to the best of these spaces

Mohammad Javad
  • 127
  • 1
  • 4