ArrayList is backed by an array. Typically, addressing something by index is assumed to be O(1), i.e., in constant time. In assembly, you can index into a memory location in constant time, as there are certain LOAD instructions that take an optional index in addition to a base address. Arrays are usually allocated in memory in a contiguous block. For example, assume you have a base address of 0x1000 (where the array starts) and you provide an index of 0x08. This means that for your array starting at 0x1000 you want to access the element at location 0x1008. The processor only needs to add the base address and the index, and look up that location in memory*. This can happen in constant time. So assume you have the following in Java:
int a = myArray[9];
Internally, the JVM will know the address of myArray. Like our example, let us assume that it is at location 0x1000. Then it knows that it needs to find the 9th subscript. So basically the location it needs to find is simply:
0x1000 + 0x09
Which gives us:
0x1009
So the machine can simply load it from there.
In C, this is actually a lot more evident. If you have an array, you can access the ith location as myArray[i] like in Java. But you can access it via pointer arithmetic too (a pointer contains an address of the actual value the pointer points to)! So if you had a pointer *ptrMyArray, you can access the ith subscript by doing *(ptrMyArray + i), which is exactly as I described: base address plus subscript!
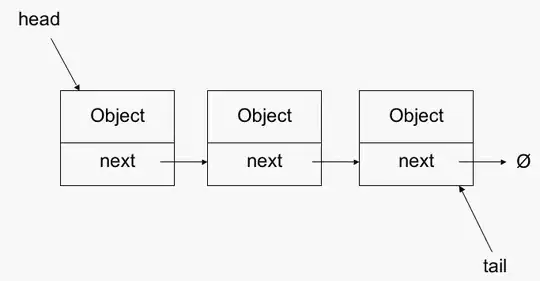
In contrast, the worst case for accessing a location in a LinkedList is O(n). If you recall your data structures, a linked list usually has a head and a tail pointer, and each node has a next pointer to the next node. So to find a node, you have to start with head and then inspect each node in turn until you get to the right one. You cannot simply index into a location either since there is no guarantee that the nodes of the linked list are next to each other in memory; they could be anywhere.
*Indexing must also take into account the size of the element, since you have to take into account how much space each element is taking. The basic example I provided assumes that each element only takes up a byte. But if you have larger elements, the formula is basically BASE_ADDRESS + (ELEMENT_SIZE_IN_BYTES * INDEX). In our case, where we assume a size of 1 byte, the formula reduces to BASE_ADDRESS + INDEX.