Generating All Binary Search Trees from 1 to n

Question

I ran into the following problem:

Given a positive integer n, generate all binary search trees with nodes 1, 2, ..., n.

For example, given 3, one obtains:

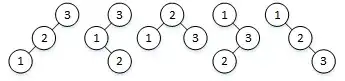
enter image description here

I am doing the following:

Generate all the permutations of the sequence (1, 2, ..., n).
For each permutation p:
    Create a tree t.
    For each number n in p:
        Insert n into t.
    If t has not yet been generated, keep it. <-- Expensive Operation

However, this approach is slow because duplicate trees are generated (for n = 3, (2, 1, 3) and (2, 3, 1) generate the same tree), and I need to ensure they are not kept. Would someone point me toward a faster approach?

you can find efficient algorithm in the answer to this question http://stackoverflow.com/questions/16004723/number-of-binary-search-trees-over-n-distinct-elements — ile, Dec 06 '13 at 23:39
possible duplicate of [Enumerate search trees](http://stackoverflow.com/questions/1483365/enumerate-search-trees) — Raymond Chen, Dec 07 '13 at 00:35
there is a simple mapping described there, which can be implemented efficieny to enumerate them all. — ile, Dec 07 '13 at 17:54

Vikram Bhat · Accepted Answer · 2014-11-07T05:57:58.127

5

Here is pseudo code to do it without duplicates(But u would still need lots of space because no of tree generate is high).

TreeList void genAllBST(int high,int low) {

  if(high>=low) {
      currList = []
      for(int i=low;i<=high;i++) {
          curr = new Node(i);
          leftList = genAllBST(i-1,low);
          rightList = genAllBST(high,i+1);
          TreeList c = connect(curr,leftList,rightList);  
          currList.add(c);
      }

     return(currList);

  }

   return(null);
}

genAllBST(n,1);

edited Nov 07 '14 at 05:57

answered Dec 07 '13 at 17:58

Vikram Bhat

6,106
3
20
19

Could you please define "TreeList", "ConnectedList", and "connect"? Thanks. – Scott Odle Nov 07 '14 at 00:39
@ScottOdle TreeList is list of trees with point to their roots , ConnectedList should be TreeList sorry for that , connect function makes all possible trees with curr as root and one from leftList as left subtree and one from rightList as right subtree – Vikram Bhat Nov 07 '14 at 06:03

Generating All Binary Search Trees from 1 to n

1 Answers1