For my d3 project, I have a series of adjacent polygons, and I want to compute a new polygon that is the outside border of all the smaller polygons put together.
I have merged all the points of several connected polygons into one array to create one large polygon. But this includes all the interior edges as well as the exterior ones. I would like to remove the inner edges of this merged polygon, so that I only have a single shape representing the outside border of the area, but I can't find a proper algorithm that does this.
I found this, but it requires that the vertices of the polygon already be explicitly known; all I have is a set of points, with no distinction between outer and inner.
Once I've removed the inner points of the resulting polygon, I'd like to draw a line with "cardinal" interpolation around the outer points. This is why I must keep the integrity of the points rather than converting the polygon to arcs and using something like topojson.mesh!
Here's a screenshot to explain more clearly:
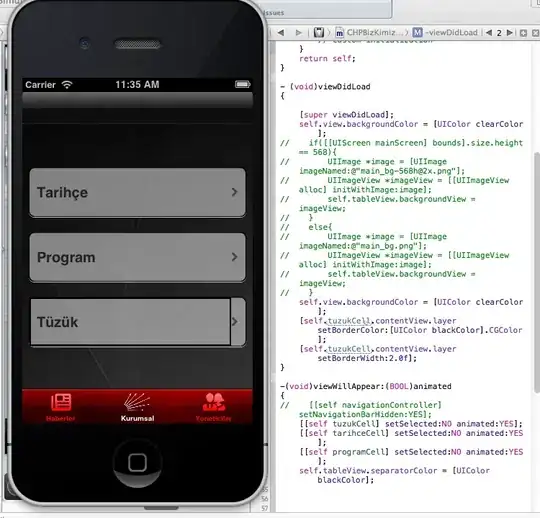
All of the vertex-points (corners of the red lines) of the green polygons were concatenated into one array of points. I want to figure out how to remove the inner points so that I can then apply a "cardinal" interpolated line around the remaining, outer points.