A Dependency Free Multiclass Confusion Matrix
# A Simple Confusion Matrix Implementation
def confusionmatrix(actual, predicted, normalize = False):
"""
Generate a confusion matrix for multiple classification
@params:
actual - a list of integers or strings for known classes
predicted - a list of integers or strings for predicted classes
normalize - optional boolean for matrix normalization
@return:
matrix - a 2-dimensional list of pairwise counts
"""
unique = sorted(set(actual))
matrix = [[0 for _ in unique] for _ in unique]
imap = {key: i for i, key in enumerate(unique)}
# Generate Confusion Matrix
for p, a in zip(predicted, actual):
matrix[imap[p]][imap[a]] += 1
# Matrix Normalization
if normalize:
sigma = sum([sum(matrix[imap[i]]) for i in unique])
matrix = [row for row in map(lambda i: list(map(lambda j: j / sigma, i)), matrix)]
return matrix
The approach here is to pair up the unique classes found in the actual vector into a 2-dimensional list. From there, we simply iterate through the zipped actual and predicted vectors and populate the counts using the indices to access the matrix positions.
Usage
cm = confusionmatrix(
[1, 1, 2, 0, 1, 1, 2, 0, 0, 1], # actual
[0, 1, 1, 0, 2, 1, 2, 2, 0, 2] # predicted
)
# And The Output
print(cm)
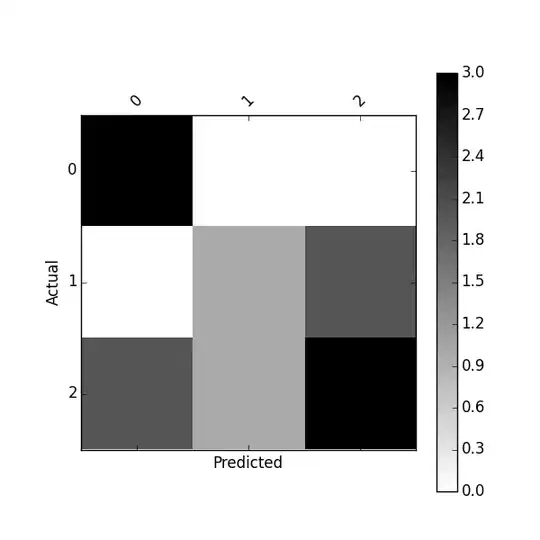
[[2, 1, 0], [0, 2, 1], [1, 2, 1]]
Note: the actual classes are along the columns and the predicted classes are along the rows.
# Actual
# 0 1 2
# # #
[[2, 1, 0], # 0
[0, 2, 1], # 1 Predicted
[1, 2, 1]] # 2
Class Names Can be Strings or Integers
cm = confusionmatrix(
["B", "B", "C", "A", "B", "B", "C", "A", "A", "B"], # actual
["A", "B", "B", "A", "C", "B", "C", "C", "A", "C"] # predicted
)
# And The Output
print(cm)
[[2, 1, 0], [0, 2, 1], [1, 2, 1]]
You Can Also Return The Matrix With Proportions (Normalization)
cm = confusionmatrix(
["B", "B", "C", "A", "B", "B", "C", "A", "A", "B"], # actual
["A", "B", "B", "A", "C", "B", "C", "C", "A", "C"], # predicted
normalize = True
)
# And The Output
print(cm)
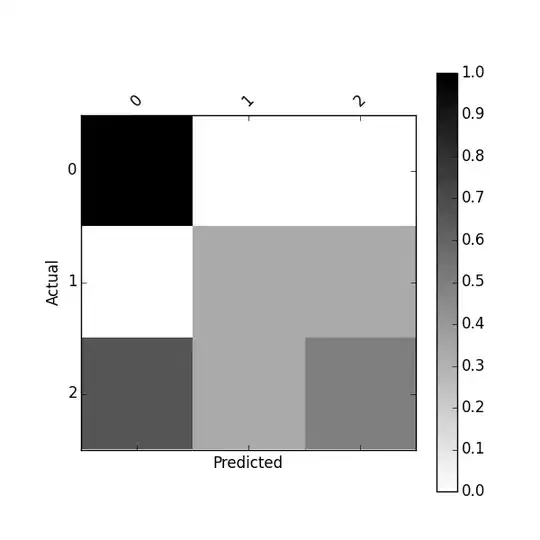
[[0.2, 0.1, 0.0], [0.0, 0.2, 0.1], [0.1, 0.2, 0.1]]
A More Robust Solution
Since writing this post, I've updated my library implementation to be a class that uses a confusion matrix representation internally to compute statistics, in addition to pretty printing the confusion matrix itself. See this Gist.
Example Usage
# Actual & Predicted Classes
actual = ["A", "B", "C", "C", "B", "C", "C", "B", "A", "A", "B", "A", "B", "C", "A", "B", "C"]
predicted = ["A", "B", "B", "C", "A", "C", "A", "B", "C", "A", "B", "B", "B", "C", "A", "A", "C"]
# Initialize Performance Class
performance = Performance(actual, predicted)
# Print Confusion Matrix
performance.tabulate()
With the output:
===================================
Aᴬ Bᴬ Cᴬ
Aᴾ 3 2 1
Bᴾ 1 4 1
Cᴾ 1 0 4
Note: classᴾ = Predicted, classᴬ = Actual
===================================
And for the normalized matrix:
# Print Normalized Confusion Matrix
performance.tabulate(normalized = True)
With the normalized output:
===================================
Aᴬ Bᴬ Cᴬ
Aᴾ 17.65% 11.76% 5.88%
Bᴾ 5.88% 23.53% 5.88%
Cᴾ 5.88% 0.00% 23.53%
Note: classᴾ = Predicted, classᴬ = Actual
===================================