Is there a simple way to find out if a point is inside a voronoi cell?
For example, the following code generates something like the diagram below:
using namespace boost::polygon;
point_data<int> p1(0, 0);
point_data<int> p2(-10, 10);
point_data<int> p3(-10, -10);
point_data<int> p4(10, -10);
point_data<int> p5(10, 10);
std::vector<point_data<int>> pts = { p1, p2, p3, p4, p5 };
construct_voronoi(pts.begin(), pts.end(), vd);
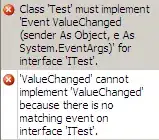
In this case, how can I found out if the point (5,5) is inside the central cell?
I could create a polygon out of each cell and find out using a point in polygon algorithm, but I'm interested in knowing the library offers something "for free".