I tried this for many hours and I keep arriving at log(logn) (where log is base 2) but this does not agree with Masters Theorem which maintains it would be just log(n).
3 Answers
Master's Theorem doesn't apply here, as we aren't dividing the input by a constant at each step. Your answer is correct.
- 560
- 2
- 11
In order to apply the Master Theorem, we have to be dividing by a constant at each step. We can still use it in this case, but we have to transform the problem.
Let k=log n, where the logarithm is base b, and define S(k)=T(b^k). Then S(k)=T(b^k)=T(n)=T(n^{1/2})+1=T((b^k)^{1/2})+1=T(b^{k/2})+1=S(k/2)+1, and we can apply the Master theorem to S, which tells us that S(k)=Theta(log k). Therefore, T(n)=T(b^{log n})=S(log n)=Theta(log(log n)), as you found.
- 4,331
- 5
- 35
- 58
People correctly suggested you that masters theorem does not work here.
To solve your problem you have to start unrolling the recursion:  .
.
The recursion will at some point stop, so we have to find a reasonable stopping point. Trying 0, 1, 2, you can see that 2 looks good, because you can easily solve the equation: 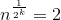 .
.
So the recursion will continue log(log(n)) times and this is your time complexity.
P.S. a little bit harder recurrence was solved here.
- 1
- 1
- 214,103
- 147
- 703
- 753