All answers to the question suggest using intersection over union (IoU) metric. This is a vectorized version of IoU that can be used for multiple roi matching.
function [IoU, match] = rectIoU(R1, R2, treshold)
I = rectint(R1, R2);
A1 = R1(:, 3).*R1(:, 4);
A2 = R2(:, 3).*R2(:, 4);
U = bsxfun(@plus, A1, A2')-I;
IoU = I./U;
if nargout > 1
if nargin<3
treshold = 0.5;
end
match = IoU>treshold;
end
end
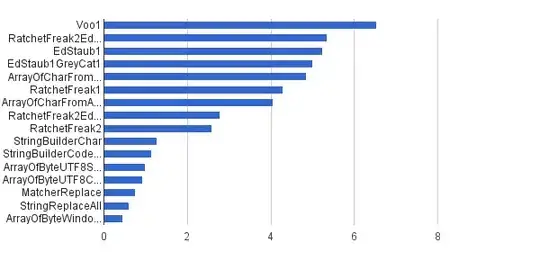
It calculates pairwise IoU for two sets of bounding boxes. If R1 and R2 each specify one rectangle, the output IoU is a scalar.
R1 and R2 can also be matrices, where each row is a position vector ([x y w h]). IoU is then a matrix giving the IoU of all rectangles specified by R1 with all the rectangles specified by R2. That is, if R1 is n-by-4 and R2 is m-by-4, then IoU is an n-by-m matrix where IoU(i,j) is the IoU of the rectangles specified by the ith row of R1 and the jth row of R2.
It also accepts a scalar parameter, treshold, to set the match output. Size of match is exactly like IoU. match(i,j) indicates if the rectangles specified by the ith row of R1 and the jth row of R2 match.
For example,
R1 = [0 0 1 1; 2 1 1 1];
R2 = [-.5 2 1 1; flipud(R1)];
R2 = R2+rand(size(R2))*.4-.2;
[IoU, match] = rectIoU(R1, R2, 0.4)
returns:
IoU =
0 0 0.7738
0 0.6596 0
match =
0 0 1
0 1 0
that means R1(1, :) and R1(2, :) match R2(3, :) and R2(2, :) respectively.
PS:
At the time I'm posting this answer, there is a small mistake in Parag's answer (the accepted answer above). IMHO they calculate the union area in a wrong way. The unionCoords in their answer is actually the blue square in the picture below, and unionArea is its area, that obviously is not the union area of red and green rectangles.