What is a SPATIAL INDEX and when should I use it?

Question

Like most of the average PHP web developers I use MySql as a RDBMS. MySql (as other RDBMS also) offers SPATIAL INDEX features, but I'm don't get it very well. I have googled for it but didn't find clear real world examples to clarify my bad knowledge about it.

Could someone explain me a little bit what is a SPATIAL INDEX and when should I use it?

Answer 1

You can use a spatial index for indexing geo-objects - shapes. The spatial index makes it possible to efficiently search for objects that overlap in space

Answer 2

Spatial Index is like an ordinary index with this difference that Spatial objects are not 1D data points rather are in higher dimension space (e.g. 2D) and thus Ordinary indexes such as BTree are not appropriate for indexing such data. The well-known spatial Index technique is R-tree ( Google it on wikipedia )

Answer 3

When we need to store some geographic data for storing locations OR we need to store shape related data then we can use it.

For Instance, Imagine that you are trying to develop an application that helps people find restaurants, pubs, bars and other hangout places near them. In nutshell, this will be a location discovery platform.

Looking from a back-end perspective, we would be needing to store geographic data of these locations like Latitude and Longitude. Then we would need to write functions that calculate the distance between the user and the location (to show how far the location is from him/her). Using the same function, we can design an algorithm that finds closest places near to the user or within a given radius from him/her.

You may find the better idea with example over here :- https://medium.com/sysf/playing-with-geometry-spatial-data-type-in-mysql-645b83880331

Answer 4

Spatial indices allow you to query with inequalities on multiple columns efficiently

E.g., with a spatial index you would be able to efficiently query all points that are inside a rectangle such as:

create table t(id integer primary key, x integer, y integer)
select * from mytable where x >= 1 and x < 10 and y >= 2 and y < 20

which has inequalities on both x and y.

The more basic and common B-tree index only allows you to efficiently speed up inequalities in one dimension, even if you try to use composite indices on x and y.

E.g. a x-y composite B-tree index would:

• efficiently speed up:
  • x = 1 and y = 2: equalities in both columns
  • x = 1 and y > 2: equality on first column plus inequality on the second column
• very limited speed up:
  • x > 1 and y > 2: inequalities on both columns, including the first
  • x > 1 and y = 2: inequality on the first column
  • y > 2: this is equivalent to x > -infinity and y > 2, so it is just the worse case possible for the compound B-tree index. Note however, this case could be solved efficiently with a B-tree index.

A spatial index would efficiently handle all the above queries however.

Example of why a composite index B-tree search would be slow

This is well explained at: https://dba.stackexchange.com/questions/249848/why-we-cant-have-more-than-one-inequality-condition-in-mysql-indexing/249909#249909

One way to visualize a B-tree is to see how it would sort the rows. After all, it is a structure analogous to a binary search tree, just with more entries per node to speed up disk access:

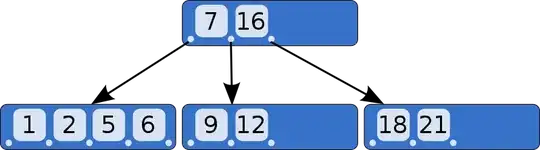
Image source

Consider the following x-y composite index, which sorts all rows by (x, y) tuples lexicographically:

x|y

1|1
1|2
1|3
1|4
1|5
1|6

2|2
2|2
2|2
2|3
2|3
2|3
2|4
2|4
2|4

4|2
4|2
4|2
4|3
4|3
4|3
4|4
4|4
4|4

5|3
5|4
5|5
5|6
5|7
5|8

And remember that the in-disk ordering might have nothing to do with this. In particular, there could be other columns with completely different values.

Now suppose we want to find:

x > 0 and y > 4

The only speedup operation we can do is a binary search on the above index.

First it uses the index to binary tree searches for (1, 5), which is a speedup over a full scan.

Then it follows the index ordering and grabs every larger y for x = 1. So far so good.

The problem is what happens next.

Note how in this case, there are no y > 4 for x = 2 and x = 4.

However, there is no way to immediately tell that from the index and jump straight to x = 5!

What the search has to do is simply: I'm done with x = 1, so now give me the next larger x. So it keeps traversing the index tree linearly until the next value.

Then it finds the first (2, 2) and it knows: OK, there exists x = 2. Now it has two choices:

• keep following the index until y = 5 is found
• binary search down to (2, 5)

Which is better depends on how many rows in total there are in the DB, since the fresh binary search is log(n), so would not be worth if unless there's a large number of values with x = 2 and y < 5.

With either of those, it decides that there were no results for x = 2, so we've just spent some time scanning a bunch of invalid rows.

So it continues the above procedure, basically scanning through the entire index.

x = 4 like x = 2 is scanned uselessly and has no reults.

Then it continues going through the index and finds x = 5, eventually reaching (5, 5), and we finally have some results.

So as we can see, this requires a lot of stepping over ranges that may not contain any results of interest, which is why this compound B-tree index can only produce a limited speedup if we are searching over a large x range with many empty y hits.

An R-tree implementation of a spatial index looks more like this:

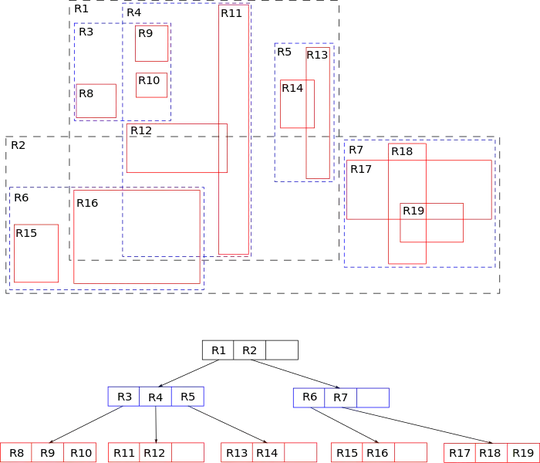
Image source

So we intuitively understand that it actually tries to split up a 2D space into a bunch of balanced rectangles, and because of that is able to efficiently query arbitrary rectangular areas.

SQLite minimal benchmark

I'm not very familiar with MySQL, but the concepts should be analogous.

I'm going to create two test databases with 10 million points in a straight line with inclination 2:

• one with a x-y B-tree index, SQLite's default index
• one with a x-y R-tree index, SQLite's built-in spatial index

And then let's ask the question:

how many points are there between x >= 1000000 and x < 2000000 and y >= 4000000 and y < 6000000

with a query:

time sqlite3 100mr.sqlite 'select count(*) from t where x >= 10000000 and x < 90000000 and y >= 50000000 and y < 60000000'

• B-tree: query: 6.4s, index creation time: 4 mins, DB file size: 3.9 GB
• R-tree: query: 0.7s, index creation time: 30 mins, DB file size: 5.9 GB

The test databases were generated as follows:

r-tree:

from pathlib import Path
import csv
import sqlite3

f = '100mr.sqlite'
n = 100000000
Path(f).unlink(missing_ok=True)
connection = sqlite3.connect(f)
cursor = connection.cursor()
cursor.execute('CREATE VIRTUAL TABLE t using rtree(id, x, x2, y, y2)')
cursor.executemany('INSERT INTO t VALUES (?, ?, ?, ?, ?)', ((None, str(i), str(i), str(i*2), str(i*2)) for i in range (n)))
connection.commit()
connection.close()

b-tree:

rm -f "$f"
time sqlite3 "$f" 'create table t(id integer, x integer, y integer)'
time sqlite3 "$f" 'insert into t select value as id, value as x, value * 2 as y from generate_series(0,99999999)'
time sqlite3 "$f" 'create index txy on t(x, y)'

So we see that in the case of this implementation, R-tree search was way faster, but at the cost of a much slower index creation time.

Tested on Ubuntu 23.04, Python 3.11.2, Lenovo ThinkPad P51, SSD: Samsung MZVLB512HAJQ-000L7 512GB SSD, 3 GB/s nominal speed, csvkit==1.0.7, sqlite 3.40.1.

Answer 5

The use of spacial index is best for searching exact matching value look-up,not for range scan.It is mainly supported in MyISAM tables but from MySQL 5.7.4 LAB release,it is also supported by Innodb.

References:- http://dev.mysql.com/doc/refman/5.5/en/creating-spatial-indexes.html http://mysqlserverteam.com/innodb-spatial-indexes-in-5-7-4-lab-release/