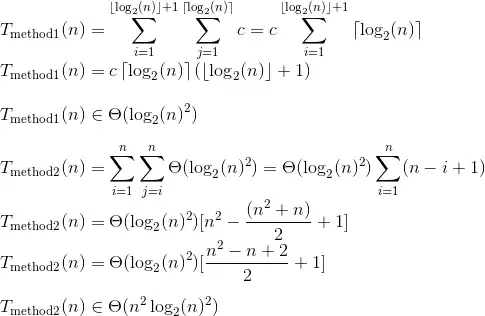What's the big-O time complexity of the two methods listed below?
Is method 1 O(log n²) or O(log n)?
Is method 2 O(n²) or something else?
public static void method1(int n) {
int k = 0;
for (int i = 1; i <= n; i = i*2)
for (int j = n; j > 1; j = j/2)
k++;
}
public static void method2(int n) {
for (int i = 1; i <= n; i = i + 1)
for (int j = i; j <= n; j++)
method1(n);
}
In the first example, the outer loop executes logn times, and the second loop also executes log n times. The complexity is O(log² n).
In the second example, the first loop executes n times and the second loop executes i times where i is the current index of the first loop. So, it executes 1 + 2 + 3 + ... + n times, summing up to n ⋅ (n - 1) / 2. The resulting complexity is O( (n² - n)/2 ) = O(n²). Read more here 1 + 2 + 3 ... series
So, to wrap it up, method2 executes method1 n² times, giving the total complexity of O(n² ⋅ log² n)
Well in the first method you have 2 nested loops where each one is exactly log(n) so yes that would turns them into a O((logn)^2)
For the second method, if we focus on the second loop we can see that for
This is an arithmetic progression and its sum is equal to n * (n+1) / 2 which turns it into an
O((nlogn)^2) since we are calling method1 about n^2 times.
The complexity of method1 is O((log n)²) since we have a nested loop where each loop runs O(log n) times.
In Method2 we execute Method1 a triangluar number of times, i.e., we execute it O(n²) times. Since we execute an O((log n)²) function O(n²) times, the resulting complexity for Method2 is O(n² ⋅ (log n)²).
Methodically and formally, you can use Sigma notation like this:
