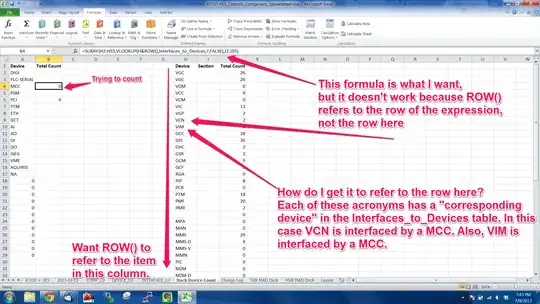
I have an ellipse, defined by Center Point, radiusX and radiusY, and I have a Point. I want to find the point on the ellipse that is closest to the given point. In the illustration below, that would be S1.
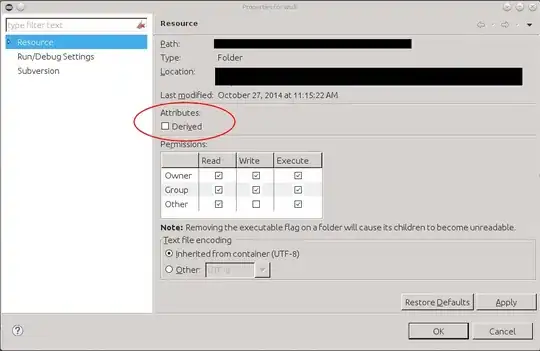
Now I already have code, but there is a logical error somewhere in it, and I seem to be unable to find it. I broke the problem down to the following code example:
#include <vector>
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <math.h>
using namespace std;
void dostuff();
int main()
{
dostuff();
return 0;
}
typedef std::vector<cv::Point> vectorOfCvPoints;
void dostuff()
{
const double ellipseCenterX = 250;
const double ellipseCenterY = 250;
const double ellipseRadiusX = 150;
const double ellipseRadiusY = 100;
vectorOfCvPoints datapoints;
for (int i = 0; i < 360; i+=5)
{
double angle = i / 180.0 * CV_PI;
double x = ellipseRadiusX * cos(angle);
double y = ellipseRadiusY * sin(angle);
x *= 1.4;
y *= 1.4;
x += ellipseCenterX;
y += ellipseCenterY;
datapoints.push_back(cv::Point(x,y));
}
cv::Mat drawing = cv::Mat::zeros( 500, 500, CV_8UC1 );
for (int i = 0; i < datapoints.size(); i++)
{
const cv::Point & curPoint = datapoints[i];
const double curPointX = curPoint.x;
const double curPointY = curPoint.y * -1; //transform from image coordinates to geometric coordinates
double angleToEllipseCenter = atan2(curPointY - ellipseCenterY * -1, curPointX - ellipseCenterX); //ellipseCenterY * -1 for transformation to geometric coords (from image coords)
double nearestEllipseX = ellipseCenterX + ellipseRadiusX * cos(angleToEllipseCenter);
double nearestEllipseY = ellipseCenterY * -1 + ellipseRadiusY * sin(angleToEllipseCenter); //ellipseCenterY * -1 for transformation to geometric coords (from image coords)
cv::Point center(ellipseCenterX, ellipseCenterY);
cv::Size axes(ellipseRadiusX, ellipseRadiusY);
cv::ellipse(drawing, center, axes, 0, 0, 360, cv::Scalar(255));
cv::line(drawing, curPoint, cv::Point(nearestEllipseX,nearestEllipseY*-1), cv::Scalar(180));
}
cv::namedWindow( "ellipse", CV_WINDOW_AUTOSIZE );
cv::imshow( "ellipse", drawing );
cv::waitKey(0);
}
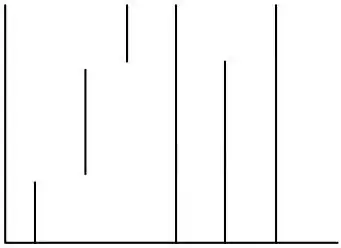
It produces the following image:
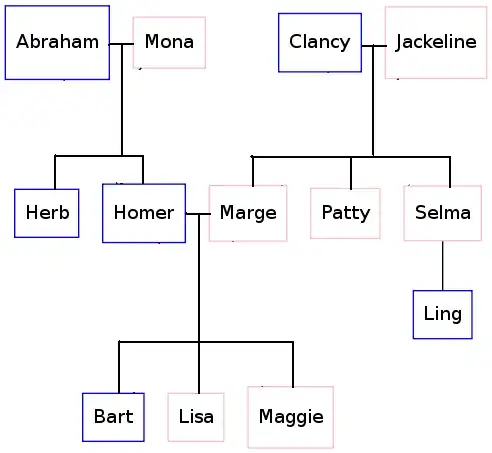
You can see that it actually finds "near" points on the ellipse, but it are not the "nearest" points. What I intentionally want is this: (excuse my poor drawing)
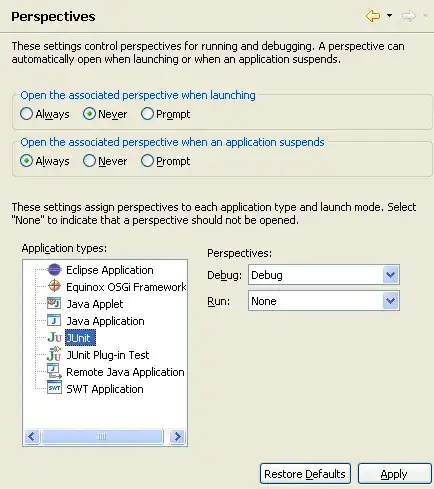
would you extent the lines in the last image, they would cross the center of the ellipse, but this is not the case for the lines in the previous image.
I hope you get the picture. Can anyone tell me what I am doing wrong?







 I proposed an stable initialization:
I proposed an stable initialization: