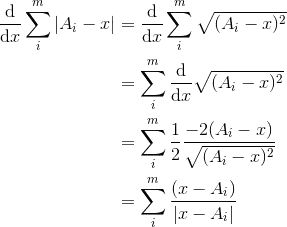Given an Array A of N non negative integers, find an integer k, such that the sum of difference of each element with k is minimum.
i.e. Summation(abs(A[i] - k)), 1 <= i <= N, or simply
|A[1] - k| + |A[2] - k| + |A[3] - k| + ... + |A[N] - k|
My Approach:
low = minimumValueInArray(A);
high= maximumValueInArray(A);
ans = Infinite;
for (k = low; k <= high; k++) {
temp = 0;
for (i = 1; i <= N; i++) {
temp += abs(A[i] - K);
}
ans = min(ans, temp);
}
return ans;
This is simply brute force approach trying to solve for all values of K.Can we optimise it.
What is the smarter way of doing this?
Reference: This was my logic behind this Codejam Round 1B problem