Opposite of ease cubic-bezier function

Question

I have the ease cubic-bezier function: cubic-bezier(.25,.1,.25,1) (http://cubic-bezier.com/#.25,.1,.25,1)

I want the opposite of this. Here is graphic representation of what I'm trying to accomplish:

The graph on left is what I have, and the function for the graph on the right is what I'm trying to achieve.

What do you mean with "opposite"? (this is not as silly a question as it sounds: bezier curves have several aspects, all of which could have an 'opposite' at any or all points). — Mike 'Pomax' Kamermans, May 04 '14 at 19:45
Oh what I mean is, i want to create a css transition that follows the curve in reverse. Curve should be exactly the same, its just that thime 0 is now at other end. — Noitidart, May 04 '14 at 20:46
CSS cubic bezier curves are defined only by two middle control points, and the first vertex is fixed at (0,0) and the last one at (1,1). https://developer.mozilla.org/en-US/docs/Web/CSS/timing-function By that definition, you can't follow the curve in reverse, can you? — hkrish, May 06 '14 at 22:07
I totally know what you mean man. I just need to make the same path from 1,1 to 0,0 be the opposite of what it was. — Noitidart, May 07 '14 at 05:36
Hi @Mike'Pomax'Kamermans I updated the post with graphic showing im trying to get. I couldn't figure it out, my math sucks :( — Noitidart, Oct 15 '14 at 03:21
Hi @hkrish updated the post with graphic showing im trying to get. I couldn't figure it out, my math sucks :( — Noitidart, Oct 15 '14 at 03:22
Ah, that's a straight up rotation about (0.5,0.5). Bezier curves are invariant under linear transforms, so you can literally just rotate all the points. I'll write up an answer with the math for that. — Mike 'Pomax' Kamermans, Oct 15 '14 at 03:27
Thank you sir!! I fail hard at math :( Btw your split function was so awesome! I modded it a bit to fit to unit cell for use in css3 :) : http://stackoverflow.com/a/26373980/1828637 — Noitidart, Oct 15 '14 at 03:37

Mike 'Pomax' Kamermans · Accepted Answer · 2014-10-15T03:51:05.530

4

If you want to do a rotation as in your updated answer, all we have to do is... well, that. Rotate around (0.5,0.5) by a 180 degree, or π radians, angle. Let's assume we have a curve encoded as an array c with four point objects { x:..., y... }, then we can effect this rotation as:

c = [ {x:...,y:...}, ..., ..., ...];

function halfUnitTurn(v) {
  // Note: it's actually 0.5 + ((v.x-0.5)*cos(pi) - (v.x-0.5)*sin(pi)),
  // (and x*sin + y*cos for the y:... part) but: cos(pi) is just -1, and
  // sin(pi) is 0, so things REALLY simplify!
  return {
    x: 0.5 - (v.x-0.5),
    y: 0.5 - (v.y-0.5)
  };
}

var rotated = c.map(function(p) { return halfUnitTurn(p); });

And as demonstrator code: http://jsfiddle.net/mokg77fq/

edited Oct 15 '14 at 03:51

answered Oct 15 '14 at 03:45

Mike 'Pomax' Kamermans

49,297
16
112
153

So awesome!! I really enjoy that math though once i understand and especially when i find an application for it! :) You got done in <10min what i couldnt do in months haha :P you can just do the `v.x-.5` cuz the `cos(pi)` is `1` huh? edit: oh yeah i see you stated that in the comment so cool! thx man!! :) – Noitidart Oct 15 '14 at 03:46
1

yeah, on quarter, half, three quarter and full rotations, the cos/sin rules become various terms 1, 0, and -1 so they make the functions *really* simple. – Mike 'Pomax' Kamermans Oct 15 '14 at 03:47
i updated fiddle for my ease function so cool looking! thank you man! http://jsfiddle.net/mokg77fq/2/ – Noitidart Oct 15 '14 at 03:54
updated here so other it makes sense to other noobs like me :) http://jsfiddle.net/mokg77fq/3/ and removed that `console.log` – Noitidart Oct 15 '14 at 04:00
Why not just `x: 1-v.x` etc? It also makes it easier to see what's going on IMHO: just flipping x and y rather than rotating (unnecessary complexity?) – Henrik Christensen May 08 '15 at 11:51
mostly because that would reduce this answer's educational value by hiding the fact that we're rotating, by optimizing too soon. No one said you should copy-paste an answer and then never try to further improve it, replacing `0.5 - (x-0.5)` with `1-X` is an obvious optimization, but certainly not one that's going to *actually* improve performance to the point where showing the simplified rotation is using bad code =) – Mike 'Pomax' Kamermans May 08 '15 at 15:19

score 2 · Answer 2 · edited Feb 08 '17 at 14:56

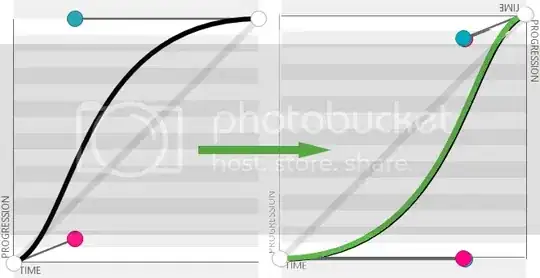
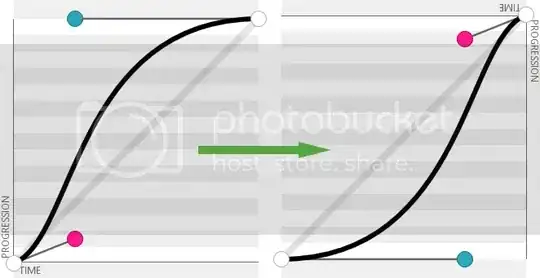
Here is Mike's awesome code put into a reusable function:

function reverseCssCubicBezier(cubicBezier) {
    var maxX = Math.max(cubicBezier[0].x, cubicBezier[1].x, cubicBezier[2].x, cubicBezier[3].x);
    var maxY = Math.max(cubicBezier[0].y, cubicBezier[1].y, cubicBezier[2].y, cubicBezier[3].y);
    var halfUnitTurn = function(v) {
        var tx = maxX/2, ty = maxY/2;
        return { x: tx - (v.x-tx), y: ty - (v.y-ty) };
    };
    var revd = cubicBezier.map(halfUnitTurn);
    return revd.reverse();
}

And this is how to use it:

var ease = [{x:0,y:0}, {x:.25,y:.1}, {x:.25,y:1}, {x:1,y:1}]; //cubic-bezier(.25, .1, .25, 1)
var ease_reversed = reverseCssCubicBezier(ease);
var ease_css_string = 'cubic_bezier(' + [ease[1].x, ease[1].y, ease[2].x, ease[2].y].join(', ') + ')';
var ease_reversed_css_string = 'cubic_bezier(' + [ease_reversed[1].x, ease_reversed[1].y, ease_reversed[2].x, ease_reversed[2].y].join(', ') + ')';

This returns:

ease: [{x:0, y:0}, {x:0.25, y:0.1}, {x:0.25, y:1}, {x:1, y:1}]
ease-reversed: [{x:0, y:0}, {x:0.75, y:0}, {x:0.75, y:0.9}, {x:1, y:1}]

ease: cubic_bezier(0.25, 0.1, 0.25, 1)
ease-reversed: cubic_bezier(0.75, 0, 0.75, 0.9)

Graphically we see its perfect overlap, i shifted the green one to left a little bit to show its perfectly overlapping.

Thanks Mike!

score 1 · Answer 3 · answered Aug 27 '23 at 15:39

What about this much simpler solution?

const reverseCurve = curve => [1 - curve[2], 1 - curve[3], 1 - curve[0], 1 - curve[1]];

const bezierCurve = [.25, .1, .25, 1]; // cubic-bezier(.25,.1,.25,1)
const reversedBezierCurve = reverseCurve(bezierCurve);

console.log(reversedBezierCurve); // [.75, 0, .75, .9]

Opposite of ease cubic-bezier function

3 Answers3