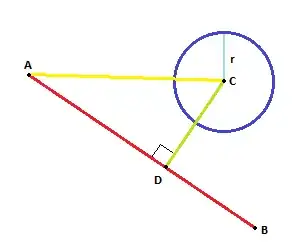
Let's think of A, B, C and D as Vectors and let
* for 2 vectors be the scalar product, i.e. the result is the sum of the products of the corresponding coordinates of the operands, and
|X| be the length of vector x, i.e. the square root of the sum of the squared values of the coordiantes of X
First we find the plane P (for 2D space the plane is a line) ortogonal to F = (B-A), that contains C:
This plane is described by the following equation (where Z is arbitrary point in the plane):
F * Z = F * C
The equation for the line G from A to B is (tin real numbers):
F * t + A
To intersect P and G you have to solve the following equation:
(F * t + A) * F = F * C
t * |F|^2 + A * F = F * C
t * |F|^2 = F * C - A * F
t = (F * (C - A)) / (|F|^2)
t = ((B - A) * (C - A)) / (|B-A|^2)
To get D insert t into G:
D = F * t + A
= (B-A) * t + A
In a 2D space, you get
ca1 = C1-A1
ca2 = C2-A2
ba1 = B1-A1
ba2 = B2-A2
t = (ba1 * ca1 + ba2 * ca2) / (ba1 * ba1 + ba2 * ba2)
D1 = ba1 * t + A1
D2 = ba2 * t + A2
Where C1 and C2 are the coordinates of C,
A1 and A2 are the coordinates of A, ect.