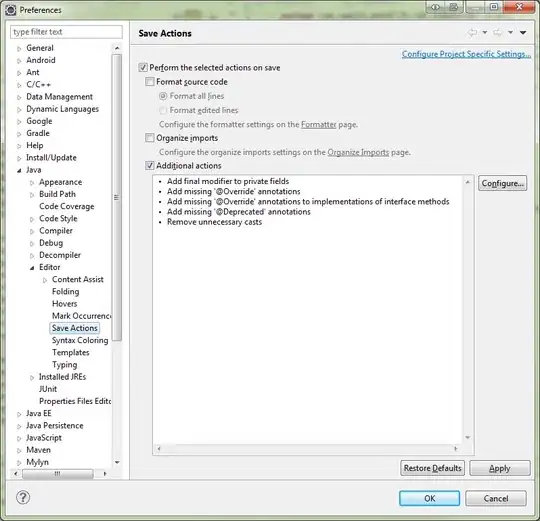
I know that there are several similar questions such as Use of curve_fit to fit data but the answer there (specific float type) does not seem to work for me. I am wondering if anyone is able to explain to me why the following code (which is an adaptation from an answer -> https://stackoverflow.com/a/11507723/1093485) does not work.
sample code:
#! /usr/bin/env python
import numpy
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
def gaussFunction(x, A, mu, sigma):
return A*numpy.exp(-(x-mu)**2/(2.*sigma**2))
x_points = [4245.428, 4245.4378, 4245.4477, 4245.4575, 4245.4673, 4245.4772, 4245.487, 4245.4968, 4245.5066, 4245.5165, 4245.5263, 4245.5361, 4245.546, 4245.5558, 4245.5656, 4245.5755, 4245.5853, 4245.5951, 4245.605, 4245.6148, 4245.6246, 4245.6345, 4245.6443, 4245.6541, 4245.6639, 4245.6738, 4245.6836, 4245.6934, 4245.7033, 4245.7131, 4245.7229, 4245.7328, 4245.7426, 4245.7524, 4245.7623, 4245.7721, 4245.7819, 4245.7918, 4245.8016, 4245.8114, 4245.8213, 4245.8311, 4245.8409, 4245.8508, 4245.8606, 4245.8704, 4245.8803, 4245.8901, 4245.8999, 4245.9097, 4245.9196, 4245.9294, 4245.9392, 4245.9491, 4245.9589, 4245.9687, 4245.9786, 4245.9884, 4245.9982, 4246.0081, 4246.0179, 4246.0277, 4246.0376, 4246.0474, 4246.0572, 4246.0671, 4246.0769, 4246.0867, 4246.0966, 4246.1064, 4246.1162, 4246.1261, 4246.1359, 4246.1457, 4246.1556, 4246.1654, 4246.1752, 4246.1851, 4246.1949, 4246.2047, 4246.2146]
y_points = [978845.0, 1165115.0, 1255368.0, 1253901.0, 1199857.0, 1134135.0, 1065403.0, 977347.0, 866444.0, 759457.0, 693284.0, 679772.0, 696896.0, 706494.0, 668272.0, 555221.0, 374547.0, 189968.0, 161754.0, 216483.0, 181937.0, 73967.0, 146627.0, 263495.0, 284992.0, 240291.0, 327541.0, 555690.0, 758847.0, 848035.0, 800159.0, 645769.0, 444412.0, 249627.0, 125078.0, 254856.0, 498501.0, 757049.0, 977861.0, 1125316.0, 1202892.0, 1263220.0, 1366361.0, 1497071.0, 1559804.0, 1464012.0, 1196896.0, 848736.0, 584363.0, 478640.0, 392943.0, 312466.0, 355540.0, 320666.0, 114711.0, 690948.0, 1409389.0, 1825921.0, 1636486.0, 1730980.0, 4081179.0, 7754166.0, 11747734.0, 15158681.0, 17197366.0, 17388832.0, 15710571.0, 12593935.0, 8784968.0, 5115720.0, 2277684.0, 769734.0, 674437.0, 647250.0, 708156.0, 882759.0, 833756.0, 504655.0, 317790.0, 711106.0, 1011705.0]
# Try to fit the gaussian
trialX = numpy.linspace(x_points[0],x_points[-1],1000)
coeff, var_matrix = curve_fit(gaussFunction, x_points, y_points)
yEXP = gaussFunction(trialX, *coeff)
# Plot the data (just for visualization)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x_points, y_points, 'b*')
plt.plot(trialX,yEXP, '--')
plt.show()
The output that it generates: