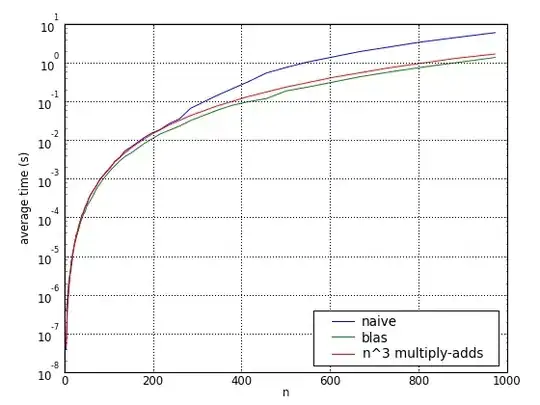
We can do matrix multiplication in several ways. A and B are two matrix, of size 1000 * 1000.
- Use the matlab builtin matrix operator.
A*B - Write two nests explicitly.
- Write three nests explicitly.
- Dynamically link C code to do the three nests.
The result is
*operator is very fast. It takes about 1 second.- Nests are very slow, especially three nests, 500 seconds.
- C Loops are much faster than the matlab nests, 10 seconds.
Can anyone explain the following. Why * is so fast and why C loops is more efficient than write the loops in matlab.
I used another software , not matlab , to do the computing. But I think similar reasoning should apply.