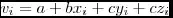C/C++: Multiply, or bitshift then divide?

Question

Where it's possible to do so, I'm wondering if it's faster to replace a single multiplication with a bitshift followed by an integer division. Say I've got an int k and I want to multiply it by 2.25.

What's faster?

int k = 5;
k *= 2.25;
std::cout << k << std::endl;

or

int k = 5;
k = (k<<1) + (k/4);
std::cout << k << std::endl;

Output

11
11

Both give the same result, you can check this full example.

Answer 1

The first attempt

I defined functions regularmultiply() and bitwisemultiply() as follows:

int regularmultiply(int j)
{
    return j * 2.25;
}

int bitwisemultiply(int k)
{
    return (k << 1) + (k >> 2);
}

Upon doing profiling with Instruments (in XCode on a 2009 Macbook OS X 10.9.2), it seemed that bitwisemultiply executed about 2x faster than regularmultiply.

The assembly code output seemed to confirm this, with bitwisemultiply spending most of its time on register shuffling and function returns, while regularmultiply spent most of its time on the multiplying.

regularmultiply:

bitwisemultiply:

But the length of my trials was too short.

The second attempt

Next, I tried executing both functions with 10 million multiplications, and this time putting the loops in the functions so that all the function entry and leaving wouldn't obscure the numbers. And this time, the results were that each method took about 52 milliseconds of time. So at least for a relatively large but not gigantic number of calculations, the two functions take about the same time. This surprised me, so I decided to calculate for longer and with larger numbers.

The third attempt

This time, I only multiplied 100 million through 500 million by 2.25, but the bitwisemultiply actually came out slightly slower than the regularmultiply.

The final attempt

Finally, I switched the order of the two functions, just to see if the growing CPU graph in Instruments was perhaps slowing the second function down. But still, the regularmultiply performed slightly better:

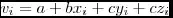
Here is what the final program looked like:

#include <stdio.h>

int main(void)
{
    void regularmultiplyloop(int j);
    void bitwisemultiplyloop(int k);

    int i, j, k;

    j = k = 4;
    bitwisemultiplyloop(k);
    regularmultiplyloop(j);

    return 0;
}

void regularmultiplyloop(int j)
{
    for(int m = 0; m < 10; m++)
    {
        for(int i = 100000000; i < 500000000; i++)
        {
            j = i;
            j *= 2.25;
        }
        printf("j: %d\n", j);
    }
}

void bitwisemultiplyloop(int k)
{
    for(int m = 0; m < 10; m++)
    {
        for(int i = 100000000; i < 500000000; i++)
        {
            k = i;
            k = (k << 1) + (k >> 2);
        }
        printf("k: %d\n", k);
    }
}

Conclusion

So what can we say about all this? One thing we can say for certain is that optimizing compilers are better than most people. And furthermore, those optimizations show themselves even more when there are a lot of computations, which is the only time you'd really want to optimize anyway. So unless you're coding your optimizations in assembly, changing multiplication to bit shifting probably won't help much.

It's always good to think about efficiency in your applications, but the gains of micro-efficiency are usually not enough to warrant making your code less readable.

Answer 2

Indeed it depends on a variety of factors. So I have just checked it by running and measuring time. So the string we are interested in takes only a few instructions of CPU which is very fast so I have wrapped it into the cycle - multiplied the execution time of one code by a big number, and I got the k *= 2.25; is about in 1.5 times slower than k = (k<<1) + (k/4);. Here is my two codes to comapre:

prog1:

#include <iostream>
using namespace std;

int main() {

int k = 5;
for (unsigned long i = 0; i <= 0x2fffffff;i++)
 k = (k<<1) + (k/4);
cout << k << endl;

return 0;
}

prog 2:

#include <iostream>
using namespace std;

int main() {

int k = 5;
for (unsigned long i = 0; i <= 0x2fffffff;i++)
 k *= 2.25;
cout << k << endl;

return 0;
}

Prog1 takes 8 secs and Prog2 takes 14 secs. So by running this test with you architecture and compiler you can get the result which is correct to your particular environment.

Answer 3

That depends heavily on the CPU architecture: Floating point arithmetic, including multiplications, has become quite cheap on many CPUs. But the necessary float->int conversion can bite you: on POWER-CPUs, for instance, the regular multiplication will crawl along due to the pipeline flushes that are generated when a value is moved from the floating point unit to the integer unit.

On some CPUs (including mine, which is an AMD CPU), this version is actually the fastest:

k *= 9;
k >>= 2;

because these CPUs can do a 64 bit integer multiplication in a single cycle. Other CPUs are definitely slower with my version than with your bitshift version, because their integer multiplication is not as heavily optimized. Most CPUs aren't as bad on multiplications as they used to be, but a multiplication can still take more than four cycles.

So, if you know which CPU your program will run on, measure which is fastest. If you don't know, your bitshift version won't perform badly on any architecture (unlike both the regular version and mine), which makes it a really safe bet.

Answer 4

It highly depends on what hardware are you using. On modern hardware floating point multiplications may run way faster than integer ones, so you might want to change the entire algorithm and start using doubles instead of integers. If you're writing for modern hardware and you have a lot of operations like multiplying by 2.25, I'd suggest using double rather than integers, if nothing else prevents you from doing that.

And be data driven - measure performance, because it's affected by compiler, hardware and your way of implementing your algorithm.