One of the most useful cases I find for linked lists working in performance-critical fields like mesh and image processing, physics engines, and raytracing is when using linked lists actually improves locality of reference and reduces heap allocations and sometimes even reduces memory use compared to the straightforward alternatives.
Now that can seem like a complete oxymoron that linked lists could do all that since they're notorious for often doing the opposite, but they have a unique property in that each list node has a fixed size and alignment requirements which we can exploit to allow them to be stored contiguously and removed in constant-time in ways that variable-sized things cannot.
As a result, let's take a case where we want to do the analogical equivalent of storing a variable-length sequence which contains a million nested variable-length sub-sequences. A concrete example is an indexed mesh storing a million polygons (some triangles, some quads, some pentagons, some hexagons, etc) and sometimes polygons are removed from anywhere in the mesh and sometimes polygons are rebuilt to insert a vertex to an existing polygon or remove one. In that case, if we store a million tiny std::vectors, then we end up facing a heap allocation for every single vector as well as potentially explosive memory use. A million tiny SmallVectors might not suffer this problem as much in common cases, but then their preallocated buffer which isn't separately heap-allocated might still cause explosive memory use.
The problem here is that a million std::vector instances would be trying to store a million variable-length things. Variable-length things tend to want a heap allocation since they cannot very effectively be stored contiguously and removed in constant-time (at least in a straightforward way without a very complex allocator) if they didn't store their contents elsewhere on the heap.
If, instead, we do this:
struct FaceVertex
{
// Points to next vertex in polygon or -1
// if we're at the end of the polygon.
int next;
...
};
struct Polygon
{
// Points to first vertex in polygon.
int first_vertex;
...
};
struct Mesh
{
// Stores all the face vertices for all polygons.
std::vector<FaceVertex> fvs;
// Stores all the polygons.
std::vector<Polygon> polys;
};
... then we've dramatically reduced the number of heap allocations and cache misses. Instead of requiring a heap allocation and potentially compulsory cache misses for every single polygon we access, we now only require that heap allocation when one of the two vectors stored in the entire mesh exceeds their capacity (an amortized cost). And while the stride to get from one vertex to the next might still cause its share of cache misses, it's still often less than if every single polygon stored a separate dynamic array since the nodes are stored contiguously and there's a probability that a neighboring vertex might be accessed prior to eviction (especially considering that many polygons will add their vertices all at once which makes the lion's share of polygon vertices perfectly contiguous).
Here is another example:
... where the grid cells are used to accelerate particle-particle collision for, say, 16 million particles moving every single frame. In that particle grid example, using linked lists we can move a particle from one grid cell to another by just changing 3 indices. Erasing from a vector and pushing back to another can be considerably more expensive and introduce more heap allocations. The linked lists also reduce the memory of a cell down to 32-bits. A vector, depending on implementation, can preallocate its dynamic array to the point where it can take 32 bytes for an empty vector. If we have around a million grid cells, that's quite a difference.
... and this is where I find linked lists most useful these days, and I specifically find the "indexed linked list" variety useful since 32-bit indices halve the memory requirements of the links on 64-bit machines and they imply that the nodes are stored contiguously in an array.
Often I also combine them with indexed free lists to allow constant-time removals and insertions anywhere:
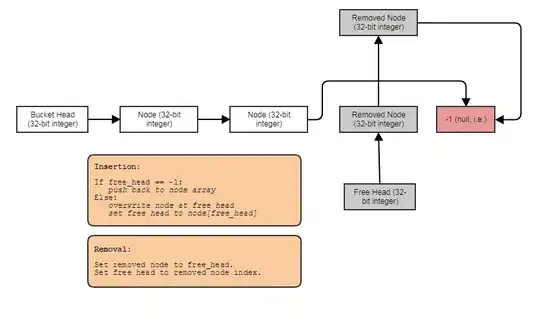
In that case, the next index either points to the next free index if the node has been removed or the next used index if the node has not been removed.
And this is the number one use case I find for linked lists these days. When we want to store, say, a million variable-length sub-sequences averaging, say, 4 elements each (but sometimes with elements being removed and added to one of these sub-sequences), the linked list allows us to store 4 million linked list nodes contiguously instead of 1 million containers which are each individually heap-allocated: one giant vector, i.e., not a million small ones.

