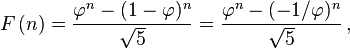Test if a number is fibonacci

Question

I know how to make the list of the Fibonacci numbers, but i don't know how can i test if a given number belongs to the fibonacci list - one way that comes in mind is generate the list of fib. numbers up to that number and see if it belongs to the array, but there's got to be another, simpler and faster method.

Any ideas ?

Answer 1

A very nice test is that N is a Fibonacci number if and only if 5 N^2 + 4 or 5N^2 – 4 is a square number. For ideas on how to efficiently test that a number is square refer to the SO discussion.

Answer 2

A positive integer ω is a Fibonacci number if and only if either 5ω² + 4 or 5ω² - 4 is a perfect square.

See The Fabulous Fibonacci Numbers for more.

Answer 3

While several people point out the perfect-square solution, it involves squaring a Fibonacci number, frequently resulting in a massive product.

There are less than 80 Fibonacci numbers that can even be held in a standard 64-bit integer.

Here is my solution, which operates entirely smaller than the number to be tested.
(written in C#, using basic types like double and long. But the algorithm should work fine for bigger types.)

static bool IsFib(long T, out long idx)
{
    double root5 = Math.Sqrt(5);
    double phi = (1 + root5) / 2;

    idx    = (long)Math.Floor( Math.Log(T*root5) / Math.Log(phi) + 0.5 );
    long u = (long)Math.Floor( Math.Pow(phi, idx)/root5 + 0.5);

    return (u == T);
}

---

More than 4 years after I wrote this answer, a commenter asked about the second parameter, passed by out.

Parameter #2 is the "Index" into the Fibonacci sequence.
If the value to be tested, T is a Fibonacci number, then idx will be the 1-based index of that number in the Fibonacci sequence. (with one notable exception)

The Fibonacci sequence is 1 1 2 3 5 8 13, etc.
3 is the 4th number in the sequence: IsFib(3, out idx); will return true and value 4.
8 is the 6th number in the sequence: IsFib(8, out idx); will return true and value 6.
13 is the 7th number; IsFib(13, out idx); will return true and value 7.

The one exception is IsFib(1, out idx);, which will return 2, even though the value 1 appears at both index 1 and 2.

If IsFib is passed a non-Fibonacci number, it will return false, and the value of idx will be the index of the biggest Fibonacci number less than T.

16 is not a Fibonacci value.
IsFib(16, out idx); will return false and value 7.
You can use Binet's Formula to convert index 7 into Fibonacci value 13, which is the largest number less than 16.

Answer 4

#!/bin/bash
victim="144"
curl http://aux.planetmath.org/files/objects/7680/fib.txt | sed 's/^[0-9]*//;s/[ \t]//g' | grep "^$victim$" >/dev/null 2>/dev/null
if [[ $? -eq 0 ]] ; then
    echo "$victim is a fibonacci number"
else
    echo "$victim aint"
fi

Answer 5

Positive integer ω is a Fibonacci number

If and only if one of 5ω² + 4 and 5ω² - 4 is a perfect square

from The (Fabulous) FIBONACCI Numbers by Alfred Posamentier and Ingmar Lehmann

bool isFibonacci(int  w)
{
       double X1 = 5 * Math.Pow(w, 2) + 4;
       double X2 = 5 * Math.Pow(w, 2) - 4;

       long X1_sqrt = (long)Math.Sqrt(X1);
       long X2_sqrt = (long)Math.Sqrt(X2);   

       return (X1_sqrt*X1_sqrt == X1) || (X2_sqrt*X2_sqrt == X2) ;
}

I copied it from this source

---

Snippet that prints Fibonacci numbers between 1k and 10k.

for (int i = 1000; i < 10000; i++)
{
         if (isFibonacci(i))
              Console.Write(" "+i);
}

OMG There are only FOUR!!!

With other method

from math import *

phi = 1.61803399
sqrt5 = sqrt(5)

def F(n):
    return int((phi**n - (1-phi)**n) /sqrt5)

def isFibonacci(z):
    return F(int(floor(log(sqrt5*z,phi)+0.5))) == z

print [i for i in range(1000,10000) if isFibonacci(i)]

Answer 6

If your numbers are of bounded size, than simply putting all fibonacci numbers below the upper bound into a hashtable and testing containment will do the trick. There are very few fibonacci numbers (for example, only 38 below 5mln), since they grow exponentially.

If your numbers are not of bounded size, then the suggested trick with square testing will almost surely be slower than generating the fibonacci sequence until the number is found or exceeded.

Answer 7

Towards a solution, take a look at Binet's Formula.
(Look for "Closed-Form Expression" under Fibonacci Number on Wikipedia)

It says that the sequence of Fibonacci Number's is created by a simple closed formula:

I believe if you solve for n, and test if n is an integer, you'll have your answer.

Edit As @psmears points out, the same Wikipedia article also has a section on detecting Fibonacci numbers. Wikipedia is an excellent source.

Answer 8

See the section "Recognizing Fibonacci numbers" on the wikipedia article about the Fibonacci numbers.

Answer 9

Since Fibonacci numbers grow exponentially, the method you suggest is pretty fast. Another is this.

Answer 10

Based on earlier answers by me and psmears, I've written this C# code.

It goes through the steps slowly, and it can clearly be reduced and optimized:

// Input: T: number to test.
// Output: idx: index of the number in the Fibonacci sequence.
//    eg: idx for 8 is 6. (0, 1, 1, 2, 3, 5, 8)
// Return value: True if Fibonacci, False otherwise.
static bool IsFib(long T, out int idx)
{
    double root5 = Math.Sqrt(5);
    double PSI = (1 + root5) / 2;

    // For reference, IsFib(72723460248141) should show it is the 68th Fibonacci number

    double a;

    a = T*root5;
    a = Math.Log(a) / Math.Log(PSI);
    a += 0.5;
    a = Math.Floor(a);
    idx = (Int32)a;

    long u = (long)Math.Floor(Math.Pow(PSI, a)/root5 + 0.5);

    if (u == T)
    {
        return true;
    }
    else
    {
        idx = 0;
        return false;
    }
}

Testing reveals this works for the first 69 Fibonacci numbers, but breaks down for the 70th.

F(69) = 117,669,030,460,994 - Works
F(70) = 190,392,490,709,135 - Fails

In all, unless you're using a BigInt library of some kind, it is probably better to have a simple lookup table of the Fibonacci Numbers and check that, rather than run an algorithm.

A list of the first 300 Numbers is readily available online.

But this code does outline a workable algorithm, provided you have enough precision, and don't overflow your number representation system.

Answer 11

Re: Ahmad's code - a simpler approach with no recursion or pointers, fairly naive, but requires next to no computational power for anything short of really titanic numbers (roughly 2N additions to verify the Nth fib number, which on a modern machine will take milliseconds at worst)

// returns pos if it finds anything, 0 if it doesn't (C/C++ treats any value !=0 as true, so same end result)

int isFib (long n)
{
    int pos = 2;
    long last = 1;
    long current = 1;
    long temp;

    while (current < n)
    {
        temp = last;
        last = current;
        current = current + temp;
        pos++;
    }

    if (current == n)
        return pos;
    else
        return 0;

}

Answer 12

From Wikipedia: http://en.wikipedia.org/wiki/Fibonacci_number

A positive integer z is a Fibonacci number if and only if one of 5z^2 + 4 or 5z^2 − 4 is a perfect square.

Answer 13

The general expression for a Fibonacci number is F(n) = [ [(1+sqrt(5))/2] sup n+1 - [(1-sqrt(5))/2] sup n+1 ]/ sqrt(5) ..... (*) The second exponential goes to zero for large n and carrying out the numerical operations we get F(n) = [ (1.618) sup n+1 ] / 2.236

If K is the number to be tested log(k*2.2336)/log(1.618) should be an integer!

Example for K equal to 13 my calculator gives the answer 7.00246 For K equal 14 the answer is 7.1564.

You can increase the confidence in the result by taking the closest integer to the answer and substitute in (*) to confirm that the result is K

Answer 14

This is my solution I'm not sure if it benchmarks. I hope this helps!

def is_fibonacci?(i)
  a,b=0,1
    until b >= i
        a,b=b,a+b
        return true if b == i
    end
end

what a,b=b,a+b is doing

 0, 1 = 1, 0 +1
 1, 1 = 1, 1 + 1
 1, 2 = 2, 1 + 2
 2, 3 = 3, 2 + 3

fib1 = fib2
fib2 = fib1 + fib2

Answer 15

A Scala version-

def isFib(n: Int): Boolean = {

def checkFib(f1: Int = 1, f2: Int = 1): Boolean = {

if(n == f1 || n == f2) true
else if(n < f2) false
else checkFib(f2, f1+f2)

}

checkFib()

}

Answer 16

Java solution can be done as below. But still it can be optimized

The following solution works for

1. 1≤T≤10 ^5
2. 1≤N≤10 ^10

T is no.of test cases, N is range of number

    import java.util.Scanner;
    import java.math.BigDecimal;
    import java.math.RoundingMode;

    public class FibonacciTester {
        private static BigDecimal zero = BigDecimal.valueOf(0);
        private static BigDecimal one = BigDecimal.valueOf(1);
        private static BigDecimal two = BigDecimal.valueOf(2);
        private static BigDecimal four = BigDecimal.valueOf(4);
        private static BigDecimal five = BigDecimal.valueOf(5);

        public static void main(String[] args) {
            Scanner sc = new Scanner(System.in);
            int n = sc.nextInt();
            BigDecimal[] inputs = new BigDecimal[n];
            for (int i = 0; i < n; i++) {
                inputs[i] = sc.nextBigDecimal();
            }

            for (int i = 0; i < inputs.length; i++) {
                if (isFibonacci(inputs[i]))
                    System.out.println("IsFibo");
                else
                    System.out.println("IsNotFibo");
            }


        }

        public static boolean isFibonacci(BigDecimal num) {
            if (num.compareTo(zero) <= 0) {
                return false;
            }

            BigDecimal base = num.multiply(num).multiply(five);
            BigDecimal possibility1 = base.add(four);
            BigDecimal possibility2 = base.subtract(four);


            return (isPerfectSquare(possibility1) || isPerfectSquare(possibility2));
        }

        public static boolean isPerfectSquare(BigDecimal num) {
            BigDecimal squareRoot = one;
            BigDecimal square = one;
            BigDecimal i = one;
            BigDecimal newSquareRoot;
            int comparison = -1;

            while (comparison != 0) {
                if (comparison < 0) {
                    i = i.multiply(two);
                    newSquareRoot = squareRoot.add(i).setScale(0, RoundingMode.HALF_UP);
                } else {
                    i = i.divide(two);
                    newSquareRoot = squareRoot.subtract(i).setScale(0, RoundingMode.HALF_UP);
                }

                if (newSquareRoot.compareTo(squareRoot) == 0) {
                    return false;
                }

                squareRoot = newSquareRoot;
                square = squareRoot.multiply(squareRoot);
                comparison = square.compareTo(num);
            }

            return true;
        }
    }

Answer 17

How big are the numbers you're dealing with?

Could a lookup table work for you? (a precomputed list of numbers you can search in)

There's also a closed-form expression that I guess you could invert to get at the answer analytically (though I'm no mathematician, so I can't promise this suggestion makes sense)

Answer 18

I ran some benchmarks on the methods presented here along with simple addition, pre-computing an array, and memoizing the results in a hash. For Perl, at least, the squaring method is a little bit faster than the logarithmic method, perhaps 20% faster. As abelenky points out, it's a tradeoff between whether you've got the room for squaring bit numbers.

Certainly, the very fastest way is to hash all the Fibonacci numbers in your domain space. Along the lines of another point that abelenky makes, there are only 94 of these suckers that are less than 2^64.

You should just pre-compute them, and put them in a Perl hash, Python dictionary, or whatever.

The properties of Fibonacci numbers are very interesting, but using them to determine whether some integer in a computer program is one is kind of like writing a subroutine to compute pi every time the program starts.

Answer 19

All answers are basically given. I would like to add a very fast C++ example code.

The basis is the lookup mechanism that has been mentioned here several times already.

With Binet's formula, we can calculate that there are only very few Fibonacci numbers that will fit in a C++ unsigned long long data type, which has usually 64 bit now in 2021. Roundabout 93. That is nowadays a really low number.

With modern C++ 17 (and above) features, we can easily create an std::array of all Fibonacci numbers for a 64bit data type at compile time.

So, we will spend only 93*8= 744 BYTE of none-runtime memory for our lookup array.

And then use std::binary_search for finding the value. So, the whole function will be:

bool isFib(const unsigned long long numberToBeChecked) {
    return std::binary_search(FIB.begin(), FIB.end(), numberToBeChecked);
}

FIB is a compile time, constexpr std::array. So, how to build that array?

We will first define the default approach for calculation a Fibonacci number as a constexpr function:

// Constexpr function to calculate the nth Fibonacci number
constexpr unsigned long long getFibonacciNumber(size_t index) noexcept {
    // Initialize first two even numbers 
    unsigned long long f1{ 0 }, f2{ 1 };

    // Calculating Fibonacci value 
    while (index--) {
        // get next value of Fibonacci sequence 
        unsigned long long f3 = f2 + f1;
        // Move to next number
        f1 = f2;
        f2 = f3;
    }
    return f2;
}

With that, Fibonacci numbers can easily be calculated at runtime. Then, we fill a std::array with all Fibonacci numbers. We use also a constexpr and make it a template with a variadic parameter pack.

We use std::integer_sequence to create a Fibonacci number for indices 0,1,2,3,4,5, ....

That is straigtforward and not complicated:

template <size_t... ManyIndices>
constexpr auto generateArrayHelper(std::integer_sequence<size_t, ManyIndices...>) noexcept {
    return std::array<unsigned long long, sizeof...(ManyIndices)>{ { getFibonacciNumber(ManyIndices)... } };
};

This function will be fed with an integer sequence 0,1,2,3,4,... and return a std::array<unsigned long long, ...> with the corresponding Fibonacci numbers.

We know that we can store maximum 93 values. And therefore we make a next function, that will call the above with the integer sequence 1,2,3,4,...,92,93, like so:

constexpr auto generateArray() noexcept {
    return generateArrayHelper(std::make_integer_sequence<size_t, MaxIndexFor64BitValue>());
}

And now, finally,

constexpr auto FIB = generateArray();

will give us a compile-time std::array<unsigned long long, 93> with the name FIB containing all Fibonacci numbers. And if we need the i'th Fibonacci number, then we can simply write FIB[i]. There will be no calculation at runtime.

---

The whole example program will look like this:

#include <iostream>
#include <array>
#include <utility>
#include <algorithm>
#include <iomanip>
// ----------------------------------------------------------------------
// All the following will be done during compile time

// Constexpr function to calculate the nth Fibonacci number
constexpr unsigned long long getFibonacciNumber(size_t index) noexcept {
    // Initialize first two even numbers 
    unsigned long long f1{ 0 }, f2{ 1 };

    // calculating Fibonacci value 
    while (index--) {
        // get next value of Fibonacci sequence 
        unsigned long long f3 = f2 + f1;
        // Move to next number
        f1 = f2;
        f2 = f3;
    }
    return f2;
}
// We will automatically build an array of Fibonacci numbers at compile time
// Generate a std::array with n elements 
template <size_t... ManyIndices>
constexpr auto generateArrayHelper(std::integer_sequence<size_t, ManyIndices...>) noexcept {
    return std::array<unsigned long long, sizeof...(ManyIndices)>{ { getFibonacciNumber(ManyIndices)... } };
};

// Max index for Fibonaccis that for an 64bit unsigned value (Binet's formula)
constexpr size_t MaxIndexFor64BitValue = 93;

// Generate the required number of elements
constexpr auto generateArray()noexcept {
    return generateArrayHelper(std::make_integer_sequence<size_t, MaxIndexFor64BitValue>());
}

// This is an constexpr array of all Fibonacci numbers
constexpr auto FIB = generateArray();

// All the above was compile time
// ----------------------------------------------------------------------


// Check, if a number belongs to the Fibonacci series
bool isFib(const unsigned long long numberToBeChecked) {
    return std::binary_search(FIB.begin(), FIB.end(), numberToBeChecked);
}

// Test
int main() {

    const unsigned long long testValue{ 498454011879264ull };

    std::cout << std::boolalpha << "Does '" <<testValue << "' belong to Fibonacci series?  --> " << isFib(498454011879264) << '\n';

    return 0;
}

---

Developed and tested with Microsoft Visual Studio Community 2019, Version 16.8.2

Additionally tested with gcc 10.2 and clang 11.0.1

Language: C++ 17

Answer 20

#include <stdio.h>
#include <math.h>

int main()
{
int number_entered, x, y;

printf("Please enter a number.\n");
scanf("%d", &number_entered);
x = y = 5 * number_entered^2 + 4;        /*Test if 5N^2 + 4 is a square number.*/
x = sqrt(x);
x = x^2;
if (x == y)
{
        printf("That number is in the Fibonacci sequence.\n");
    }
x = y = 5 * number_entered^2 - 4;        /*Test if 5N^2 - 4 is a square number.*/
x = sqrt(x);
x = x^2;
if (x == y)
{
    printf("That number is in the Fibonacci sequence.\n");
}
else
{
    printf("That number isn't in the Fibonacci sequence.\n");
}
return 0;
}

Will this work?

Answer 21

int isfib(int n /* number */, int &pos /* position */)
{
   if (n == 1)
   {
      pos=2;  // 1 1
      return 1;
   }
   else if (n == 2)
   {
      pos=3;  // 1 1 2
      return 1;
   }
   else
   {
      int m = n /2;
      int p, q, x, y;
      int t1=0, t2 =0;
      for (int i = m; i < n; i++)
      {
        p = i;
        q = n -p;    // p + q = n
        t1 = isfib(p, x);
        if (t1) t2 = isfib(q, y);
        if (t1 && t2 && x == y +1)
        {
           pos = x+1;
           return 1; //true
        }
      }
      pos = -1;
      return 0; //false
   }
}

How about this?