I am working with a hexagonal grid. I have chosen to use this coordinate system because it is quite elegant.
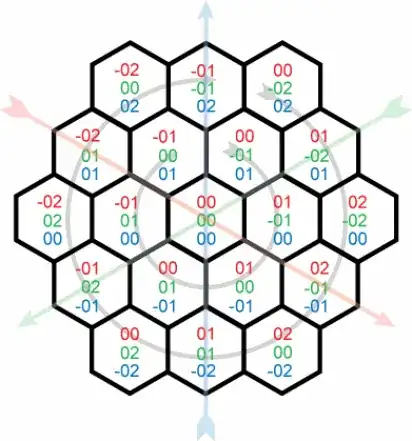
This question talks about generating the coordinates themselves, and is quite useful. My issue now is in converting these coordinates to and from actual pixel coordinates. I am looking for a simple way to find the center of a hexagon with coordinates x,y,z. Assume (0,0) in pixel coordinates is at (0,0,0) in hex coords, and that each hexagon has an edge of length s. It seems to me like x,y, and z should each move my coordinate a certain distance along an axis, but they are interrelated in an odd way I can't quite wrap my head around it.
Bonus points if you can go the other direction and convert any (x,y) point in pixel coordinates to the hex that point belongs in.