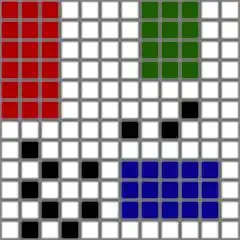
Take a look at this: Dynamic programming - Largest square block
Basically, given the rectangles, you add an obstacle, and remove the square that the obstacle interferes with.
Then, run the linked algorithm(with the "limiters" being the obstacles and existing squares), and if a place was found that can fit a square of NxN size (N is the large part of the rectangle), and add the rectangle).
This can be optimized a bit further, and I entrust you with doing so. (Basically - the rectangles won't always be put in the most optimal place. This can be remedied, at least to some degree)
This solution will give you O(n) time and space for each obstacle added.
Possible modification you should also look into: Don't rebuild the array for each obstacle, but build it for the void-of-obstacles array, and modify it as you go along. This will save going through the entire array for every single obstacle.