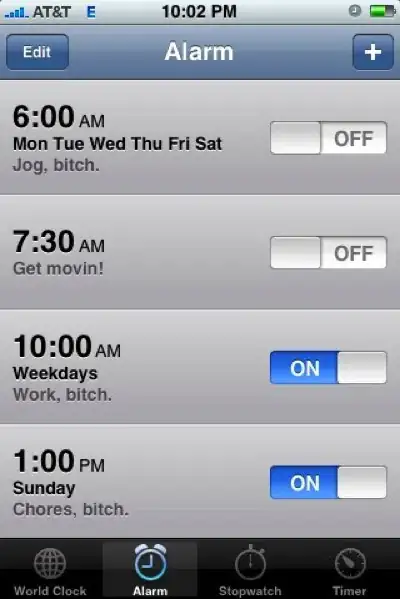
I have a large dataset of (x,y,z) protein positions and would like to plot areas of high occupancy as a heatmap. Ideally the output should look similiar to the volumetric visualisation below, but I'm not sure how to achieve this with matplotlib.
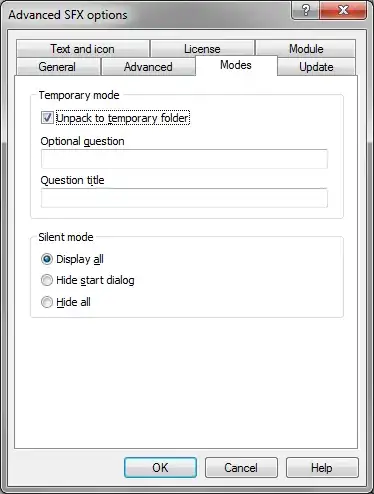
My initial idea was to display my positions as a 3D scatter plot and color their density via a KDE. I coded this up as follows with test data:
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
mu, sigma = 0, 0.1
x = np.random.normal(mu, sigma, 1000)
y = np.random.normal(mu, sigma, 1000)
z = np.random.normal(mu, sigma, 1000)
xyz = np.vstack([x,y,z])
density = stats.gaussian_kde(xyz)(xyz)
idx = density.argsort()
x, y, z, density = x[idx], y[idx], z[idx], density[idx]
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, c=density)
plt.show()
This works well! However, my real data contains many thousands of data points and calculating the kde and the scatter plot becomes extremely slow.
A small sample of my real data:
My research would suggest that a better option is to evaluate the gaussian kde on a grid. I’m just not sure how to this in 3D:
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
mu, sigma = 0, 0.1
x = np.random.normal(mu, sigma, 1000)
y = np.random.normal(mu, sigma, 1000)
nbins = 50
xy = np.vstack([x,y])
density = stats.gaussian_kde(xy)
xi, yi = np.mgrid[x.min():x.max():nbins*1j, y.min():y.max():nbins*1j]
di = density(np.vstack([xi.flatten(), yi.flatten()]))
fig = plt.figure()
ax = fig.add_subplot(111)
ax.pcolormesh(xi, yi, di.reshape(xi.shape))
plt.show()