Introduction to problem setup
I was doing some benchmarks involving - ~A and A==0for a double array with no NaNs, both of which convert A to a logical array where all zeros are converted to true values and rest are set as false values.
For the benchmarking, I have used three sets of input data –
- Very small to small sized data -
15:5:100 - Small to medium sized data -
50:40:1000 - Medium to large sized data -
200:400:3800
The input is created with A = round(rand(N)*20), where N is the parameter taken from the size array. Thus, N would vary from 15 to 100 with stepsize of 5 for the first set and similarly for the second and third sets. Please note that I am defining datasize as N, thus the number of elements would be datasize^2 or N^2.
Benchmarking Code
N_arr = 15:5:100; %// for very small to small sized input array
N_arr = 50:40:1000; %// for small to medium sized input array
N_arr = 200:400:3800; %// for medium to large sized input array
timeall = zeros(2,numel(N_arr));
for k1 = 1:numel(N_arr)
A = round(rand(N_arr(k1))*20);
f = @() ~A;
timeall(1,k1) = timeit(f);
clear f
f = @() A==0;
timeall(2,k1) = timeit(f);
clear f
end
Results

Finally the questions
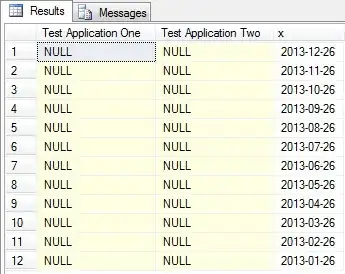
One can see how A==0 performs better than ~A across all datasizes. So here are some observations and related questions alongside them –
A==0has one relational operator and one operand, whereas~Ahas only one relational operator. Both produce logical arrays and both accept double arrays. In fact,A==0would work withNaNstoo, wheras~Awon’t. So, why is still~Aat least not as good asA==0as it looks likeA==0is doing more work or am I missing something here?There’s a peculiar drop of elapsed time with
A==0and thus increased performance atN = 320, i.e. at102400elements for A. I have observed this across many runs with that size on two different systems that I have access to. So what’s going on there?