Calculating Angles between connected line segments using MATLAB

Question

I'm using MATLAB for the first time, and I have little experience with programming.

I have three coordinate points connected together with line segments to create a sort of zig-zag path. If the line segment from the origin to the first point was extended past the first point, I need to find the angle measure from the line extending from the first point to the line extending from the first point to the second point. This needs to be done for the second to the third point as well. I've read the solutions of similar questions, but I wasn't able to interpret and modify them for my situation.

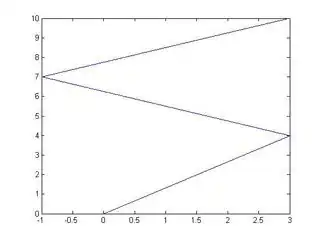
enter image description here

Related answer on calculating angle from coordinates robustly http://stackoverflow.com/a/21486462/380384 — John Alexiou, Aug 18 '14 at 18:02

Stewie Griffin · Answer 1 · 2014-08-22T09:58:50.860

Let's say your coordinates are:

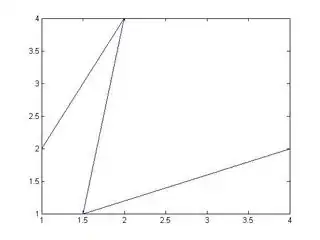
coord = [1 2; 2 4; 1.5 1; 4 2]
coord =
    1.0000    2.0000
    2.0000    4.0000
    1.5000    1.0000
    4.0000    2.0000

This will give the following zig-zag pattern:

enter image description here

To find the angles of each line segment, you can do the following:

coord_diff = diff(coord) %// Find the difference between each 
                         %// coordinate (i.e. the line between the points)

%// Make use of complex numbers. A vector is 
%// given by x + i*y, where i is the imaginary unit
vector = coord_diff(:,1) + 1i * coord_diff(:,2);

line_angles = angle(vector) * 180/pi; %// Line angles given in degrees  
diff_line_angle = diff(line_angles)   %// The difference in angle between each line segment

This gives the following angles, which upon inspection of the graph seems reasonable.

line_angles =    
   63.4349
  -99.4623
   21.8014

diff_line_angle =
 -162.8973
  121.2637

Update after comments

coord = [0 0; 3 4; -1 7; 3 10]   
coord =
     0     0
     3     4
    -1     7
     3    10

coord_diff = diff(coord) %// Find the difference between each 
                         %// coordinate (i.e. the line between the points)
coord_diff =
     3     4
    -4     3
     4     3
%// The angles of these lines are approximately 36.86 and 53.13 degrees

%// Make use of complex numbers. A vector is 
%// given by x + i*y, where i is the imaginary unit
vector = coord_diff(:,1) + 1i * coord_diff(:,2);

line_angles = angle(vector) * 180/pi; %// Line angles given in degrees
line_angles =
   53.1301
  143.1301
   36.8699

I'm not sure how you want to treat different signs etc., but something like this should work:

[90-line_angles(1), arrayfun(@(n) line_angles(n+1)-line_angles(n), ...
    1:numel(line_angles)-1)].'
ans =
   36.8699
   90.0000
 -106.2602

This is simpler, but harder to adapt in case you need to change signs or something similar:

[90-line_angles(1); diff(line_angles)]

enter image description here

Thank you for your response, but I don't think this is what I was looking for. It was my vague question that is to blame. Here are a few more details. The first segment must start at the origin and each consecutive point must have a larger Y-value than the last, creating a vertical zig-zag. Then by extending each line segment past the point at which there is a bend in the zig-zag and measuring the angle from the protruding line segment to the next coordinate. If only I had ten reputation and could post images, I'm sure it would become clear. — user1, Aug 18 '14 at 21:12
Post a link to a picture on pastebin, imgur or something similar and someone can upload it for you. But it's clearer now with the new info. I believe my answer is only minor changes away from being what you want. If the first row in the matrix is `[0 0]`, you can find what you're looking for by taking `line_angles(n)-line_angles(n-1)`. I'll update my answer later :-) — Stewie Griffin, Aug 19 '14 at 07:45
Here is a link to the image. The blue arcs are the angle measures that I need. http://imgur.com/wz15nAh Thanks for your help! — user1, Aug 19 '14 at 16:35
I don't mean to bother you, but I still can't seem to get the code to come out to the solution I get when working the problem out by hand. If you could take a look at the link to the image I posted and give me a few more pointers, I greatly appreciate it! Thanks for your help! — user1, Aug 21 '14 at 20:43
@user1, I'm not sure how you want to treat different signs, but I think the update will help you. =) — Stewie Griffin, Aug 22 '14 at 09:51

Calculating Angles between connected line segments using MATLAB

1 Answers1

Update after comments