I have set of points which lies on the image. These set of points form a irregular closed shape. I need to find the area of this shape. Does any body which is the normal algorithm used for calculating the area ? Or is there any support available in libraries such as boost? I am using C++.
-
Next time try Math Overflow (http://mathoverflow.net/) and then come back here with a question regarding the implementation of the best algorithm they give you. You'd probably get better results. – Ricket Mar 31 '10 at 13:27
-
12@Ricket: Math Overflow is for graduate-level and above research questions. This question is too easy and would be rejected. – Brian Mar 31 '10 at 13:31
-
you can try this link: http://www.wikihow.com/Calculate-the-Area-of-a-Polygon Hope it helps – N.T.C Feb 17 '13 at 11:03
7 Answers
If you polygon is simple (it doesn't have any point in common except for the pairs of consecutive segments) then wikipedia comes to help you:
The formula for the area is
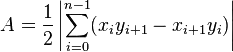
(it assumes that the last point is the same of the first one)
You can easily implement it as
float area = 0.0f;
for (int i = 0; i < numVertices - 1; ++i)
area += point[i].x * point[i+1].y - point[i+1].x * point[i].y;
area += point[numVertices-1].x * point[0].y - point[0].x * point[numVertices-1].y;
area = abs(area) / 2.0f;
Of course vertices must be ordered according to their natural following in the polygon..
-
you were, right: because the formula assumes that point[n] == point[0]. Added the last step to the algorithm. – Jack Mar 31 '10 at 13:57
-
On the second to last line, point[0] doesn't specify whether it's using X or Y. I'm assuming X, given the code in the forloop. Also, I would enclose the forloop in brackets so it's easier to read. – Stealth Rabbi Mar 17 '14 at 11:56
-
The second last line is only needed if the last point is not the same as the first one. Else it adds 0 (so having it doesn't hurt anyway). – clankill3r Nov 27 '15 at 15:26
You might want to be more precise, possibly even providing a graphical example.
For instance, if the points you have are merely pixels, then the number of pixels equals the area. But if the points are the corners of a polygon, then the area of the polygon isn't that easily determined. You'd use polygon triangulation, and sum the areas of the triangles obtained.
- 173,980
- 10
- 155
- 350
Note: If you don't know the order of the points and cannot guarantee that your polygon is convex, it is not possible to determine the ordering of the shape, since there may be more than one possible order the points which produces a polygon. If you do know that the polygon is convex, determining the ordering of the points is easy. Merely sort the points by angle from one particular point., with the first point being the one that forms a line between itself and the initial point such that all the other points are on the same side of the line. The triangles formed by this process can also be used to calculate the area.
- 25,523
- 18
- 82
- 173
There is support for area calculation of polygons in Boost.Geometry (which isn't yet accepted into boost and which is very confusing to use). Otherwise you would have to determine the polygon that is defined by your points first. From the looks of it all of your points are vertices of the polygon so this is a simply a matter of ordering your point sets correctly. Another possibility is that you are looking for the convex hull of your point set (see http://en.wikipedia.org/wiki/Convex_hull_algorithms).
- 58,701
- 10
- 113
- 156
Without modesty, I refer you to my answer to another question Combined area of overlapping circles. Monte Carlo is robust, easy-to-parallelise and will, eventually, give you an answer to the accuracy you require.
- 1
- 1
- 77,191
- 7
- 105
- 161
-
2In this case calculating the exact area is less expensive than performing *one* Monte Carlo trial. – Beta Mar 31 '10 at 13:46
-
Figuring out if a point is inside of a polygon is not any easier than just calculating the area. – Brian Mar 31 '10 at 19:55