How to draw very specific annular sectors using visual basic .NET

Question

Here goes... I need to draw several annular sectors in VisualBasic.NET using a GraphicsPath.

I would for instance enter the annular sector's outer and inner diameter/radius and a starting and ending degree/radiant. The function must then return a GraphicsPath that can simply be added to another GraphicsPath as a closed shape. This seems very easy to do, but I need it to keep a 5 pixel gap between the annular sectors.

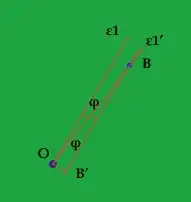
I will explain more... If for instance I enter 0 degrees as starting point and 360 degrees as ending point it must return a GraphicsPath with an annular sector that starts at X degrees (where X is 2.5 pixels offset from 0 degrees) and ends at Y degrees (where Y is -2.5 pixels offset from 360 degrees). Both the outer and inner curves of the annular sector must adhere to the above. It basically must be as if I drew two parallel lines 5 pixels apart through the circle's center at the degrees entered and used the lines as starting and ending points for the arcs. This must hold true for any Degrees entered.

This post: SVG donut slice as path element (annular sector) Almost solves the problem, but it draws all annular sectors from the center point (not unlike Pie slices) outwards causing consecutive outer rings to have bigger and bigger gaps in between if you split them with 1 Degree each time (plus it is for SVG).

I include an image explaining what I am trying to say better: https://onedrive.live.com/redir?resid=79292E5BC057FE03!112&authkey=!AMnkq0bjbsH4BwU&v=3&ithint=photo%2cjpg

This question was solved by valter. Scroll down to EDIT 2 in his answer for the code.

This image: (https://onedrive.live.com/redir?resid=79292E5BC057FE03!113&authkey=!AGxrnpf8MiiEX48&v=3&ithint=photo%2cjpg) shows what can be achieved with his solution.

The following code was used to create the GraphicsPath used to draw the pie and annular sectors in the image. At the time of writing this negative sweepA (sweep angle) was not supported.

Dim p As GraphicsPath = New GraphicsPath()
p.AddPie(160.0F, 160.0F, 280.0F, 280.0F, 300.0F, 90.0F)
p.AddPath(DrawAnnular(New Point(300I, 300I), 100I, 70I, 300.0F, 90.0F, 5.0R), False)
p.AddPath(DrawAnnular(New Point(300I, 300I), 100I, 70I, 30.0F, 80.0F, 5.0R), False)
p.AddPath(DrawAnnular(New Point(300I, 300I), 135I, 105I, 300.0F, 90.0F, 5.0R), False)
p.AddPath(DrawAnnular(New Point(300I, 300I), 135I, 105I, 30.0F, 80.0F, 5.0R), False)

Thanks

drifter

Answer 1

pntC is the center. outerR and innerR are the radius. startA and endA are the angles. The angles are measured from x axis and clockwise

Private Sub DrawAnnular(ByVal pntC As Point, ByVal outerR As Integer, ByVal innerR As Integer, ByVal startA As Integer, ByVal endA As Integer)
    Dim g As Graphics
    Dim mypen As New Pen(Color.FromKnownColor(KnownColor.Control), 1) 'the form back color
    Dim mybrush As New SolidBrush(Color.FromKnownColor(KnownColor.Control)) 'the form back color

    g = Me.CreateGraphics
    g.SmoothingMode = SmoothingMode.AntiAlias

    g.FillPie(Brushes.Black, pntC.X - outerR, pntC.Y - outerR, 2 * outerR, 2 * outerR, startA, -startA + endA) 'Outer
    g.FillPie(mybrush, pntC.X - innerR, pntC.Y - innerR, 2 * innerR, 2 * innerR, startA, -startA + endA) 'Inner

    g.DrawPie(mypen, pntC.X - outerR, pntC.Y - outerR, 2 * outerR, 2 * outerR, startA, -startA + endA) 'Outer
    g.DrawPie(mypen, pntC.X - innerR, pntC.Y - innerR, 2 * innerR, 2 * innerR, startA, -startA + endA) 'Inner

    g.Dispose()
End Sub

EDIT

This is an example of how to find the GraphicPath with the gap.

Dim pth As New GraphicsPath

pth.AddArc(outArc)

pth.AddLine(D, C)

pth.AddArc(innArc)

pth.AddLine(A, B)

and there is your path. Lets find A, B (the same logic applies to C, D):

ε1 : y = a * x + b
ε1': y = a * x + (b +- 2,5) we keep the minus in this example

a is known (the angle of ε1 with x axis) and b can be calculated (pntC belongs to ε1):

pntC.Υ = a * pntC.X + b

Now we have to find the intercept points of ε1' with outer circle(B) and with inner circle(A):

Solve these equations for x, y (point B)

circle: (x - pntC.X) * (x - pntC.X) + (y - pntC.Y) * (y - pntC.Y) = outerR * outerR
ε1'   : y = a * x + (b - 2,5)

Solve these equations for x, y (point A)

circle: (x - pntC.X) * (x - pntC.X) + (y - pntC.Y) * (y - pntC.Y) = innerR * innerR
ε1'   : y = a * x + (b - 2,5)

Now we need to valculate outArc, innArc. outArc (the same logic applies for innerArc):

pth.AddArc(outArc): pth.AddArc(pntC.X - outerR, pntC.Y - outerR, 2 * outerR, 2 * outerR, startA + φ, endA - startA - 2 * φ)

Calculating φ (OBB' triangle):

sinφ = OB'/OB => sinφ = 2,5 / outerR

One last thing. Because Form coordinates are opposite from real ones (only for Y axis), before using pntC for your calculation, convert to real one :

real: pntC.Yr = (Form client Height) - pntC.Y

and when you calculate A, B, C, D, transform to Form ones (the r means real):

A.Y = (Form client Height) - A.Yr
B.Y = (Form client Height) - B.Yr
C.Y = (Form client Height) - C.Yr
D.Y = (Form client Height) - D.Yr

EDIT 2

With the gap:

Private Sub DrawAnnular(ByVal pntC As Point, ByVal outerR As Integer, ByVal innerR As Integer, ByVal startA As Single, ByVal sweepA As Single, ByVal gap As Double)
    Dim g As Graphics
    Dim pth As New GraphicsPath
    Dim fe, dbl As Double 'fe is "φ"

    gap = gap / 2.0R

    g = Me.CreateGraphics
    g.SmoothingMode = SmoothingMode.AntiAlias

    dbl = gap / CDbl(outerR)
    fe = Math.Asin(dbl) * 180.0R / Math.PI

    pth.AddArc(pntC.X - outerR, pntC.Y - outerR, 2 * outerR, 2 * outerR, startA + CSng(fe), sweepA - CSng(2.0R * fe)) 'Outer

    dbl = gap / CDbl(innerR)
    fe= Math.Asin(dbl) * 180.0R / Math.PI

    pth.AddArc(pntC.X - innerR, pntC.Y - innerR, 2 * innerR, 2 * innerR, startA + sweepA - CSng(fe), -(sweepA - CSng(2.0R * fe))) 'Inner

    g.FillPath(Brushes.Black, pth)

    pth.Dispose()
    g.Dispose()
End Sub

valter