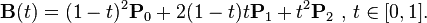I'm looking for an algorithm to find bounding box (max/min points) of a closed quadratic bezier curve in Cartesian axis:
input: C (a closed bezier curve)
output: A B C D points
Image http://www.imagechicken.com/uploads/1270586513022388700.jpg
Note: above image shows a smooth curve. it could be not smooth. (have corners)
Ivan Kuckir's DeCasteljau is a brute force, but works in many cases. The problem with it is the count of iterations. The actual shape and the distance between coordinates affect to the precision of the result. And to find a precise enough answer, you have to iterate tens of times, may be more. And it may fail if there are sharp turns in curve.
Better solution is to find first derivative roots, as is described on the excellent site http://processingjs.nihongoresources.com/bezierinfo/. Please read the section Finding the extremities of the curves.
The link above has the algorithm for both quadratic and cubic curves.
The asker of question is interested in quadratic curves, so the rest of this answer may be irrelevant, because I provide codes for calculating extremities of Cubic curves.
Below are three Javascript codes of which the first (CODE 1) is the one I suggest to use.
** CODE 1 **
After testing processingjs and Raphael's solutions I find they had some restrictions and/or bugs. Then more search and found Bonsai and it's bounding box function, which is based on NISHIO Hirokazu's Python script. Both have a downside where double equality is tested using ==. When I changed these to numerically robust comparisons, then script succeeds 100% right in all cases. I tested the script with thousands of random paths and also with all collinear cases and all succeeded:
The code is as follows. Usually left, right, top and bottom values are the all needed, but in some cases it's fine to know the coordinates of local extreme points and corresponding t values. So I added there two variables: tvalues and points. Remove code regarding them and you have fast and stable bounding box calculation function.
// Source: http://blog.hackers-cafe.net/2009/06/how-to-calculate-bezier-curves-bounding.html
// Original version: NISHIO Hirokazu
// Modifications: Timo
var pow = Math.pow,
sqrt = Math.sqrt,
min = Math.min,
max = Math.max;
abs = Math.abs;
function getBoundsOfCurve(x0, y0, x1, y1, x2, y2, x3, y3)
{
var tvalues = new Array();
var bounds = [new Array(), new Array()];
var points = new Array();
var a, b, c, t, t1, t2, b2ac, sqrtb2ac;
for (var i = 0; i < 2; ++i)
{
if (i == 0)
{
b = 6 * x0 - 12 * x1 + 6 * x2;
a = -3 * x0 + 9 * x1 - 9 * x2 + 3 * x3;
c = 3 * x1 - 3 * x0;
}
else
{
b = 6 * y0 - 12 * y1 + 6 * y2;
a = -3 * y0 + 9 * y1 - 9 * y2 + 3 * y3;
c = 3 * y1 - 3 * y0;
}
if (abs(a) < 1e-12) // Numerical robustness
{
if (abs(b) < 1e-12) // Numerical robustness
{
continue;
}
t = -c / b;
if (0 < t && t < 1)
{
tvalues.push(t);
}
continue;
}
b2ac = b * b - 4 * c * a;
sqrtb2ac = sqrt(b2ac);
if (b2ac < 0)
{
continue;
}
t1 = (-b + sqrtb2ac) / (2 * a);
if (0 < t1 && t1 < 1)
{
tvalues.push(t1);
}
t2 = (-b - sqrtb2ac) / (2 * a);
if (0 < t2 && t2 < 1)
{
tvalues.push(t2);
}
}
var x, y, j = tvalues.length,
jlen = j,
mt;
while (j--)
{
t = tvalues[j];
mt = 1 - t;
x = (mt * mt * mt * x0) + (3 * mt * mt * t * x1) + (3 * mt * t * t * x2) + (t * t * t * x3);
bounds[0][j] = x;
y = (mt * mt * mt * y0) + (3 * mt * mt * t * y1) + (3 * mt * t * t * y2) + (t * t * t * y3);
bounds[1][j] = y;
points[j] = {
X: x,
Y: y
};
}
tvalues[jlen] = 0;
tvalues[jlen + 1] = 1;
points[jlen] = {
X: x0,
Y: y0
};
points[jlen + 1] = {
X: x3,
Y: y3
};
bounds[0][jlen] = x0;
bounds[1][jlen] = y0;
bounds[0][jlen + 1] = x3;
bounds[1][jlen + 1] = y3;
tvalues.length = bounds[0].length = bounds[1].length = points.length = jlen + 2;
return {
left: min.apply(null, bounds[0]),
top: min.apply(null, bounds[1]),
right: max.apply(null, bounds[0]),
bottom: max.apply(null, bounds[1]),
points: points, // local extremes
tvalues: tvalues // t values of local extremes
};
};
// Usage:
var bounds = getBoundsOfCurve(532,333,117,305,28,93,265,42);
console.log(JSON.stringify(bounds));
// Prints: {"left":135.77684049079755,"top":42,"right":532,"bottom":333,"points":[{"X":135.77684049079755,"Y":144.86387466397255},{"X":532,"Y":333},{"X":265,"Y":42}],"tvalues":[0.6365030674846626,0,1]}
CODE 2 (which fails in collinear cases):
I translated the code from http://processingjs.nihongoresources.com/bezierinfo/sketchsource.php?sketch=tightBoundsCubicBezier to Javascript. The code works fine in normal cases, but not in collinear cases where all points lie on the same line.
For reference, here is the Javascript code.
function computeCubicBaseValue(a,b,c,d,t) {
var mt = 1-t;
return mt*mt*mt*a + 3*mt*mt*t*b + 3*mt*t*t*c + t*t*t*d;
}
function computeCubicFirstDerivativeRoots(a,b,c,d) {
var ret = [-1,-1];
var tl = -a+2*b-c;
var tr = -Math.sqrt(-a*(c-d) + b*b - b*(c+d) +c*c);
var dn = -a+3*b-3*c+d;
if(dn!=0) { ret[0] = (tl+tr)/dn; ret[1] = (tl-tr)/dn; }
return ret;
}
function computeCubicBoundingBox(xa,ya,xb,yb,xc,yc,xd,yd)
{
// find the zero point for x and y in the derivatives
var minx = 9999;
var maxx = -9999;
if(xa<minx) { minx=xa; }
if(xa>maxx) { maxx=xa; }
if(xd<minx) { minx=xd; }
if(xd>maxx) { maxx=xd; }
var ts = computeCubicFirstDerivativeRoots(xa, xb, xc, xd);
for(var i=0; i<ts.length;i++) {
var t = ts[i];
if(t>=0 && t<=1) {
var x = computeCubicBaseValue(t, xa, xb, xc, xd);
var y = computeCubicBaseValue(t, ya, yb, yc, yd);
if(x<minx) { minx=x; }
if(x>maxx) { maxx=x; }}}
var miny = 9999;
var maxy = -9999;
if(ya<miny) { miny=ya; }
if(ya>maxy) { maxy=ya; }
if(yd<miny) { miny=yd; }
if(yd>maxy) { maxy=yd; }
ts = computeCubicFirstDerivativeRoots(ya, yb, yc, yd);
for(i=0; i<ts.length;i++) {
var t = ts[i];
if(t>=0 && t<=1) {
var x = computeCubicBaseValue(t, xa, xb, xc, xd);
var y = computeCubicBaseValue(t, ya, yb, yc, yd);
if(y<miny) { miny=y; }
if(y>maxy) { maxy=y; }}}
// bounding box corner coordinates
var bbox = [minx,miny, maxx,miny, maxx,maxy, minx,maxy ];
return bbox;
}
CODE 3 (works in most cases):
To handle also collinear cases, I found Raphael's solution, which is based on the same first derivative method as the CODE 2. I added also a return value dots, which has the extrema points, because always it's not enough to know bounding boxes min and max coordinates, but we want to know the exact extrema coordinates.
EDIT: found another bug. Fails eg. in 532,333,117,305,28,93,265,42 and also many other cases.
The code is here:
Array.max = function( array ){
return Math.max.apply( Math, array );
};
Array.min = function( array ){
return Math.min.apply( Math, array );
};
var findDotAtSegment = function (p1x, p1y, c1x, c1y, c2x, c2y, p2x, p2y, t) {
var t1 = 1 - t;
return {
x: t1*t1*t1*p1x + t1*t1*3*t*c1x + t1*3*t*t * c2x + t*t*t * p2x,
y: t1*t1*t1*p1y + t1*t1*3*t*c1y + t1*3*t*t * c2y + t*t*t * p2y
};
};
var cubicBBox = function (p1x, p1y, c1x, c1y, c2x, c2y, p2x, p2y) {
var a = (c2x - 2 * c1x + p1x) - (p2x - 2 * c2x + c1x),
b = 2 * (c1x - p1x) - 2 * (c2x - c1x),
c = p1x - c1x,
t1 = (-b + Math.sqrt(b * b - 4 * a * c)) / 2 / a,
t2 = (-b - Math.sqrt(b * b - 4 * a * c)) / 2 / a,
y = [p1y, p2y],
x = [p1x, p2x],
dot, dots=[];
Math.abs(t1) > "1e12" && (t1 = 0.5);
Math.abs(t2) > "1e12" && (t2 = 0.5);
if (t1 >= 0 && t1 <= 1) {
dot = findDotAtSegment(p1x, p1y, c1x, c1y, c2x, c2y, p2x, p2y, t1);
x.push(dot.x);
y.push(dot.y);
dots.push({X:dot.x, Y:dot.y});
}
if (t2 >= 0 && t2 <= 1) {
dot = findDotAtSegment(p1x, p1y, c1x, c1y, c2x, c2y, p2x, p2y, t2);
x.push(dot.x);
y.push(dot.y);
dots.push({X:dot.x, Y:dot.y});
}
a = (c2y - 2 * c1y + p1y) - (p2y - 2 * c2y + c1y);
b = 2 * (c1y - p1y) - 2 * (c2y - c1y);
c = p1y - c1y;
t1 = (-b + Math.sqrt(b * b - 4 * a * c)) / 2 / a;
t2 = (-b - Math.sqrt(b * b - 4 * a * c)) / 2 / a;
Math.abs(t1) > "1e12" && (t1 = 0.5);
Math.abs(t2) > "1e12" && (t2 = 0.5);
if (t1 >= 0 && t1 <= 1) {
dot = findDotAtSegment(p1x, p1y, c1x, c1y, c2x, c2y, p2x, p2y, t1);
x.push(dot.x);
y.push(dot.y);
dots.push({X:dot.x, Y:dot.y});
}
if (t2 >= 0 && t2 <= 1) {
dot = findDotAtSegment(p1x, p1y, c1x, c1y, c2x, c2y, p2x, p2y, t2);
x.push(dot.x);
y.push(dot.y);
dots.push({X:dot.x, Y:dot.y});
}
// remove duplicate dots
var dots2 = [];
var l = dots.length;
for(var i=0; i<l; i++) {
for(var j=i+1; j<l; j++) {
if (dots[i].X === dots[j].X && dots[i].Y === dots[j].Y)
j = ++i;
}
dots2.push({X: dots[i].X, Y: dots[i].Y});
}
return {
min: {x: Array.min(x), y: Array.min(y)},
max: {x: Array.max(x), y: Array.max(y)},
dots: dots2 // these are the extrema points
};
};
Use De Casteljau algorithm to approximate the curve of higher orders. Here is how it works for cubic curve http://jsfiddle.net/4VCVX/25/
function getCurveBounds(ax, ay, bx, by, cx, cy, dx, dy)
{
var px, py, qx, qy, rx, ry, sx, sy, tx, ty,
tobx, toby, tocx, tocy, todx, tody, toqx, toqy,
torx, tory, totx, toty;
var x, y, minx, miny, maxx, maxy;
minx = miny = Number.POSITIVE_INFINITY;
maxx = maxy = Number.NEGATIVE_INFINITY;
tobx = bx - ax; toby = by - ay; // directions
tocx = cx - bx; tocy = cy - by;
todx = dx - cx; tody = dy - cy;
var step = 1/40; // precision
for(var d=0; d<1.001; d+=step)
{
px = ax +d*tobx; py = ay +d*toby;
qx = bx +d*tocx; qy = by +d*tocy;
rx = cx +d*todx; ry = cy +d*tody;
toqx = qx - px; toqy = qy - py;
torx = rx - qx; tory = ry - qy;
sx = px +d*toqx; sy = py +d*toqy;
tx = qx +d*torx; ty = qy +d*tory;
totx = tx - sx; toty = ty - sy;
x = sx + d*totx; y = sy + d*toty;
minx = Math.min(minx, x); miny = Math.min(miny, y);
maxx = Math.max(maxx, x); maxy = Math.max(maxy, y);
}
return {x:minx, y:miny, width:maxx-minx, height:maxy-miny};
}
Well, I would say you start by adding all endpoints to your bounding box. Then, you go through all the bezier elements. I assume the formula in question is this one:
From this, extract two formulas for X and Y, respectively. Test both for extrema by taking the derivative (zero crossings). Then add the corresponding points to your bounding box as well.
I believe that the control points of a Bezier curve form a convex hull that encloses the curve. If you just want a axis-aligned bounding box, I think you need to find the min and max of each (x, y) for each control point of all the segments.
I suppose that might not be a tight box. That is, the box might be slightly larger than it needs to be, but it's simple and fast to compute. I guess it depends on your requirements.
I think the accepted answer is fine, but just wanted to offer a little more explanation for anyone else trying to do this.
Consider a quadratic Bezier with starting point p1, ending point p2 and "control point" pc. This curve has three parametric equations:
pa(t) = p1 + t(pc-p1)pb(t) = pc + t(p2-pc)p(t) = pa(t) + t*(pb(t) - pa(t))In all cases, t runs from 0 to 1, inclusive.
The first two are linear, defining line segments from p1 to pc and from pc to p2, respectively. The third is quadratic once you substitute in the expressions for pa(t) and pb(t); this is the one that actually defines points on the curve.
Actually, each of these equations is a pair of equations, one for the horizontal dimension, and one for the vertical. The nice thing about parametric curves is that the x and y can be handled independently of one another. The equations are exactly the same, just substitute x or y for p in the above equations.
The important point is that the line segment defined in equation 3, that runs from pa(t) to pb(t) for a specific value of t is tangent to the curve at the corresponding point p(t). To find the local extrema of the curve, you need to find the parameter value where the tangent is flat (i.e., a critical point). For the vertical dimension, you want to find the value of t such that ya(t) = yb(t), which gives the tangent a slope of 0. For the horizontal dimension, find t such that xa(t) = xb(t), which gives the tangent an infinite slope (i.e., a vertical line). In each case, you can just plug the value of t back into equation 1 (or 2, or even 3) to get the location of that extrema.
In other words, to find the vertical extrema of the curve, take just the y-component of equations 1 and 2, set them equal to each other and solve for t; plug this back into the y-component of equation 1, to get the y-value of that extrema. To get the complete y-range of the curve, find the minimum of this extreme y value and the y-components of the two end points, and likewise find the maximum of all three. Repeat for x to get the horizontal limits.
Remember that t only runs in [0, 1], so if you get a value outside of this range, it means there is no local extrema on the curve (at least not between your two endpoints). This includes the case where you end up dividing by zero when solving for t, which you will probably need to check for before you do it.
The same idea can be applied to higher-order Beziers, there are just more equations of higher degree, which also means there are potentially more local extrema per curve. For instance, on a cubic Bezier (two control points), solving for t to find the local extrema is a quadratic equation, so you could get 0, 1, or 2 values (remember to check for 0-denominators, and for negative square-roots, both of which indicate that there are no local extrema for that dimension). To find the range, you just need to find the min/max of all the local extrema, and the two end points.
I answered this question in Calculating the bounding box of cubic bezier curve
this article explain the details and also has a live html5 demo:
Calculating / Computing the Bounding Box of Cubic Bezier
I found a javascript in Snap.svg to calculate that: here
see the bezierBBox and curveDim functions.
I rewrite a javascript function.
//(x0,y0) is start point; (x1,y1),(x2,y2) is control points; (x3,y3) is end point.
function bezierMinMax(x0, y0, x1, y1, x2, y2, x3, y3) {
var tvalues = [], xvalues = [], yvalues = [],
a, b, c, t, t1, t2, b2ac, sqrtb2ac;
for (var i = 0; i < 2; ++i) {
if (i == 0) {
b = 6 * x0 - 12 * x1 + 6 * x2;
a = -3 * x0 + 9 * x1 - 9 * x2 + 3 * x3;
c = 3 * x1 - 3 * x0;
} else {
b = 6 * y0 - 12 * y1 + 6 * y2;
a = -3 * y0 + 9 * y1 - 9 * y2 + 3 * y3;
c = 3 * y1 - 3 * y0;
}
if (Math.abs(a) < 1e-12) {
if (Math.abs(b) < 1e-12) {
continue;
}
t = -c / b;
if (0 < t && t < 1) {
tvalues.push(t);
}
continue;
}
b2ac = b * b - 4 * c * a;
if (b2ac < 0) {
continue;
}
sqrtb2ac = Math.sqrt(b2ac);
t1 = (-b + sqrtb2ac) / (2 * a);
if (0 < t1 && t1 < 1) {
tvalues.push(t1);
}
t2 = (-b - sqrtb2ac) / (2 * a);
if (0 < t2 && t2 < 1) {
tvalues.push(t2);
}
}
var j = tvalues.length, mt;
while (j--) {
t = tvalues[j];
mt = 1 - t;
xvalues[j] = (mt * mt * mt * x0) + (3 * mt * mt * t * x1) + (3 * mt * t * t * x2) + (t * t * t * x3);
yvalues[j] = (mt * mt * mt * y0) + (3 * mt * mt * t * y1) + (3 * mt * t * t * y2) + (t * t * t * y3);
}
xvalues.push(x0,x3);
yvalues.push(y0,y3);
return {
min: {x: Math.min.apply(0, xvalues), y: Math.min.apply(0, yvalues)},
max: {x: Math.max.apply(0, xvalues), y: Math.max.apply(0, yvalues)}
};
}
Timo-s first variant adapted to Objective-C
CGPoint CubicBezierPointAt(CGPoint p1, CGPoint p2, CGPoint p3, CGPoint p4, CGFloat t) {
CGFloat x = CubicBezier(p1.x, p2.x, p3.x, p4.x, t);
CGFloat y = CubicBezier(p1.y, p2.y, p3.y, p4.y, t);
return CGPointMake(x, y);
}
// array containing TopLeft and BottomRight points for curve`s enclosing bounds
NSArray* CubicBezierExtremums(CGPoint p1, CGPoint p2, CGPoint p3, CGPoint p4) {
CGFloat a, b, c, t, t1, t2, b2ac, sqrtb2ac;
NSMutableArray *tValues = [NSMutableArray new];
for (int i = 0; i < 2; i++) {
if (i == 0) {
a = 3 * (-p1.x + 3 * p2.x - 3 * p3.x + p4.x);
b = 6 * (p1.x - 2 * p2.x + p3.x);
c = 3 * (p2.x - p1.x);
}
else {
a = 3 * (-p1.y + 3 * p2.y - 3 * p3.y + p4.y);
b = 6 * (p1.y - 2 * p2.y + p3.y);
c = 3 * (p2.y - p1.y);
}
if(ABS(a) < CGFLOAT_MIN) {// Numerical robustness
if (ABS(b) < CGFLOAT_MIN) {// Numerical robustness
continue;
}
t = -c / b;
if (t > 0 && t < 1) {
[tValues addObject:[NSNumber numberWithDouble:t]];
}
continue;
}
b2ac = pow(b, 2) - 4 * c * a;
if (b2ac < 0) {
continue;
}
sqrtb2ac = sqrt(b2ac);
t1 = (-b + sqrtb2ac) / (2 * a);
if (t1 > 0.0 && t1 < 1.0) {
[tValues addObject:[NSNumber numberWithDouble:t1]];
}
t2 = (-b - sqrtb2ac) / (2 * a);
if (t2 > 0.0 && t2 < 1.0) {
[tValues addObject:[NSNumber numberWithDouble:t2]];
}
}
int j = (int)tValues.count;
CGFloat x = 0;
CGFloat y = 0;
NSMutableArray *xValues = [NSMutableArray new];
NSMutableArray *yValues = [NSMutableArray new];
while (j--) {
t = [[tValues objectAtIndex:j] doubleValue];
x = CubicBezier(p1.x, p2.x, p3.x, p4.x, t);
y = CubicBezier(p1.y, p2.y, p3.y, p4.y, t);
[xValues addObject:[NSNumber numberWithDouble:x]];
[yValues addObject:[NSNumber numberWithDouble:y]];
}
[xValues addObject:[NSNumber numberWithDouble:p1.x]];
[xValues addObject:[NSNumber numberWithDouble:p4.x]];
[yValues addObject:[NSNumber numberWithDouble:p1.y]];
[yValues addObject:[NSNumber numberWithDouble:p4.y]];
//find minX, minY, maxX, maxY
CGFloat minX = [[xValues valueForKeyPath:@"@min.self"] doubleValue];
CGFloat minY = [[yValues valueForKeyPath:@"@min.self"] doubleValue];
CGFloat maxX = [[xValues valueForKeyPath:@"@max.self"] doubleValue];
CGFloat maxY = [[yValues valueForKeyPath:@"@max.self"] doubleValue];
CGPoint origin = CGPointMake(minX, minY);
CGPoint bottomRight = CGPointMake(maxX, maxY);
NSArray *toReturn = [NSArray arrayWithObjects:
[NSValue valueWithCGPoint:origin],
[NSValue valueWithCGPoint:bottomRight],
nil];
return toReturn;
}
Timo's CODE 2 answer has a small bug: the t parameter in computeCubicBaseValue function should be last. Nevertheless good job, works like a charm ;)
Solution in C# :
double computeCubicBaseValue(double a, double b, double c, double d, double t)
{
var mt = 1 - t;
return mt * mt * mt * a + 3 * mt * mt * t * b + 3 * mt * t * t * c + t * t * t * d;
}
double[] computeCubicFirstDerivativeRoots(double a, double b, double c, double d)
{
var ret = new double[2] { -1, -1 };
var tl = -a + 2 * b - c;
var tr = -Math.Sqrt(-a * (c - d) + b * b - b * (c + d) + c * c);
var dn = -a + 3 * b - 3 * c + d;
if (dn != 0) { ret[0] = (tl + tr) / dn; ret[1] = (tl - tr) / dn; }
return ret;
}
public double[] ComputeCubicBoundingBox(Point start, Point firstControl, Point secondControl, Point end)
{
double xa, ya, xb, yb, xc, yc, xd, yd;
xa = start.X;
ya = start.Y;
xb = firstControl.X;
yb = firstControl.Y;
xc = secondControl.X;
yc = secondControl.Y;
xd = end.X;
yd = end.Y;
// find the zero point for x and y in the derivatives
double minx = Double.MaxValue;
double maxx = Double.MinValue;
if (xa < minx) { minx = xa; }
if (xa > maxx) { maxx = xa; }
if (xd < minx) { minx = xd; }
if (xd > maxx) { maxx = xd; }
var ts = computeCubicFirstDerivativeRoots(xa, xb, xc, xd);
for (var i = 0; i < ts.Length; i++)
{
var t = ts[i];
if (t >= 0 && t <= 1)
{
var x = computeCubicBaseValue(xa, xb, xc, xd,t);
var y = computeCubicBaseValue(ya, yb, yc, yd,t);
if (x < minx) { minx = x; }
if (x > maxx) { maxx = x; }
}
}
double miny = Double.MaxValue;
double maxy = Double.MinValue;
if (ya < miny) { miny = ya; }
if (ya > maxy) { maxy = ya; }
if (yd < miny) { miny = yd; }
if (yd > maxy) { maxy = yd; }
ts = computeCubicFirstDerivativeRoots(ya, yb, yc, yd);
for (var i = 0; i < ts.Length; i++)
{
var t = ts[i];
if (t >= 0 && t <= 1)
{
var x = computeCubicBaseValue(xa, xb, xc, xd,t);
var y = computeCubicBaseValue(ya, yb, yc, yd,t);
if (y < miny) { miny = y; }
if (y > maxy) { maxy = y; }
}
}
// bounding box corner coordinates
var bbox = new double[] { minx, miny, maxx, maxy};
return bbox;
}
