Adding to the performance of different integral data types, I tested the performance of Int32 vs Int64 (i.e. int vs long) for an implementation of my prime number calculator, and found that on my x64 machine (Ryzen 1800X) there was no marked difference.
I couldn't really test with shorts (Int16 and UInt16) because it overflows pretty quickly.
And as others noted, your short loops are obfuscating your results, and especially your debugging statements. You should try to use a worker thread instead.
Here is a performance comparison of int vs long:
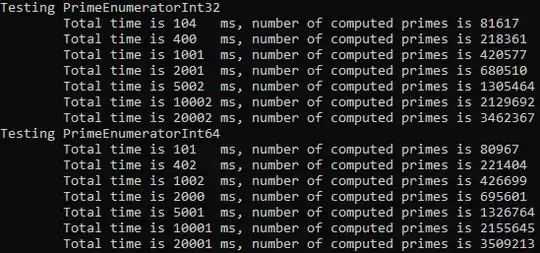
Of course, make sure to avoid long (and anything other than plain int) for array indices, since you can't even use them, and casting to int could only hurt performance (immeasurable in my test).
Here is my profiling code, which polls the progress as the worker thread spins forever. It does slow down slightly with repeated tests, so I made sure to test in other orderings and individually as well:
public static void Run() {
TestWrapper(new PrimeEnumeratorInt32());
TestWrapper(new PrimeEnumeratorInt64());
TestWrapper(new PrimeEnumeratorInt64Indices());
}
private static void TestWrapper<X>(X enumeration)
where X : IDisposable, IEnumerator {
int[] lapTimesMs = new int[] { 100, 300, 600, 1000, 3000, 5000, 10000 };
int sleepNumberBlockWidth = 2 + (int)Math.Ceiling(Math.Log10(lapTimesMs.Max()));
string resultStringFmt = string.Format("\tTotal time is {{0,-{0}}}ms, number of computed primes is {{1}}", sleepNumberBlockWidth);
int totalSlept = 0;
int offset = 0;
Stopwatch stopwatch = new Stopwatch();
Type t = enumeration.GetType();
FieldInfo field = t.GetField("_known", BindingFlags.NonPublic | BindingFlags.Instance);
Console.WriteLine("Testing {0}", t.Name);
_continue = true;
Thread thread = new Thread(InfiniteLooper);
thread.Start(enumeration);
stopwatch.Start();
foreach (int sleepSize in lapTimesMs) {
SleepExtensions.SleepWithProgress(sleepSize + offset);
//avoid race condition calling the Current property by using reflection to get private data
Console.WriteLine(resultStringFmt, stopwatch.ElapsedMilliseconds, ((IList)field.GetValue(enumeration)).Count);
totalSlept += sleepSize;
offset = totalSlept - (int)stopwatch.ElapsedMilliseconds;//synchronize to stopwatch laps
}
_continue = false;
thread.Join(100);//plz stop in time (Thread.Abort is no longer supported)
enumeration.Dispose();
stopwatch.Stop();
}
private static bool _continue = true;
private static void InfiniteLooper(object data) {
IEnumerator enumerator = (IEnumerator)data;
while (_continue && enumerator.MoveNext()) { }
}
}
Note you can replace SleepExtensions.SleepWithProgress with just Thread.Sleep
And the three variations of the algorithm being profiled:
Int32 version
class PrimeEnumeratorInt32 : IEnumerator<int> {
public int Current { get { return this._known[this._currentIdx]; } }
object IEnumerator.Current { get { return this.Current; } }
private int _currentIdx = -1;
private List<int> _known = new List<int>() { 2, 3 };
public bool MoveNext() {
if (++this._currentIdx >= this._known.Count)
this._known.Add(this.ComputeNext(this._known[^1]));
return true;//no end
}
private int ComputeNext(int lastKnown) {
int current = lastKnown + 2;//start at 2 past last known value, which is guaranteed odd because we initialize up thru 3
int testIdx;
int sqrt;
bool isComposite;
while (true) {//keep going until a new prime is found
testIdx = 1;//all test values are odd, so skip testing the first known prime (two)
sqrt = (int)Math.Sqrt(current);//round down, and avoid casting due to the comparison type of the while loop condition
isComposite = false;
while (this._known[testIdx] <= sqrt) {
if (current % this._known[testIdx++] == 0L) {
isComposite = true;
break;
}
}
if (isComposite) {
current += 2;
} else {
return current;//and end
}
}
}
public void Reset() {
this._currentIdx = -1;
}
public void Dispose() {
this._known = null;
}
}
Int64 version
class PrimeEnumeratorInt64 : IEnumerator<long> {
public long Current { get { return this._known[this._currentIdx]; } }
object IEnumerator.Current { get { return this.Current; } }
private int _currentIdx = -1;
private List<long> _known = new List<long>() { 2, 3 };
public bool MoveNext() {
if (++this._currentIdx >= this._known.Count)
this._known.Add(this.ComputeNext(this._known[^1]));
return true;//no end
}
private long ComputeNext(long lastKnown) {
long current = lastKnown + 2;//start at 2 past last known value, which is guaranteed odd because we initialize up thru 3
int testIdx;
long sqrt;
bool isComposite;
while (true) {//keep going until a new prime is found
testIdx = 1;//all test values are odd, so skip testing the first known prime (two)
sqrt = (long)Math.Sqrt(current);//round down, and avoid casting due to the comparison type of the while loop condition
isComposite = false;
while (this._known[testIdx] <= sqrt) {
if (current % this._known[testIdx++] == 0L) {
isComposite = true;
break;
}
}
if (isComposite)
current += 2;
else
return current;//and end
}
}
public void Reset() {
this._currentIdx = -1;
}
public void Dispose() {
this._known = null;
}
}
Int64 for both values and indices
Note the necessary casting of indices accessing the _known list.
class PrimeEnumeratorInt64Indices : IEnumerator<long> {
public long Current { get { return this._known[(int)this._currentIdx]; } }
object IEnumerator.Current { get { return this.Current; } }
private long _currentIdx = -1;
private List<long> _known = new List<long>() { 2, 3 };
public bool MoveNext() {
if (++this._currentIdx >= this._known.Count)
this._known.Add(this.ComputeNext(this._known[^1]));
return true;//no end
}
private long ComputeNext(long lastKnown) {
long current = lastKnown + 2;//start at 2 past last known value, which is guaranteed odd because we initialize up thru 3
long testIdx;
long sqrt;
bool isComposite;
while (true) {//keep going until a new prime is found
testIdx = 1;//all test values are odd, so skip testing the first known prime (two)
sqrt = (long)Math.Sqrt(current);//round down, and avoid casting due to the comparison type of the while loop condition
isComposite = false;
while (this._known[(int)testIdx] <= sqrt) {
if (current % this._known[(int)testIdx++] == 0L) {
isComposite = true;
break;
}
}
if (isComposite)
current += 2;
else
return current;//and end
}
}
public void Reset() {
this._currentIdx = -1;
}
public void Dispose() {
this._known = null;
}
}
Total, my test program is using 43MB of memory after 20 seconds for Int32 and 75MB of memory for Int64, due to the List<...> _known collection, which is the biggest difference I'm observing.
I profiled versions using unsigned types as well. Here are my results (Release mode):
Testing PrimeEnumeratorInt32
Total time is 20000 ms, number of computed primes is 3842603
Testing PrimeEnumeratorUInt32
Total time is 20001 ms, number of computed primes is 3841554
Testing PrimeEnumeratorInt64
Total time is 20001 ms, number of computed primes is 3839953
Testing PrimeEnumeratorUInt64
Total time is 20002 ms, number of computed primes is 3837199
All 4 versions have essentially identical performance. I guess the lesson here is to never assume how performance will be affected, and that you should probably use Int64 if you are targeting an x64 architecture, since it matches my Int32 version even with the increased memory usage.
And a validation my prime calculator is working:
P.S. Release mode had consistent results that were 1.1% faster.
P.P.S. Here are the necessary using statements:
using System;
using System.Collections;
using System.Collections.Generic;
using System.Diagnostics;
using System.Linq;
using System.Reflection;
using System.Threading;


