I have some data like
arr = [
[30.0, 0.0257],
[30.0, 0.0261],
[30.0, 0.0261],
[30.0, 0.026],
[30.0, 0.026],
[35.0, 0.0387],
[35.0, 0.0388],
[35.0, 0.0387],
[35.0, 0.0388],
[35.0, 0.0388],
[40.0, 0.0502],
[40.0, 0.0503],
[40.0, 0.0502],
[40.0, 0.0498],
[40.0, 0.0502],
[45.0, 0.0582],
[45.0, 0.0574],
[45.0, 0.058],
[45.0, 0.058],
[45.0, 0.058],
[50.0, 0.0702],
[50.0, 0.0702],
[50.0, 0.0698],
[50.0, 0.0704],
[50.0, 0.0703],
[55.0, 0.0796],
[55.0, 0.0808],
[55.0, 0.0803],
[55.0, 0.0805],
[55.0, 0.0806],
]
which is plotted like 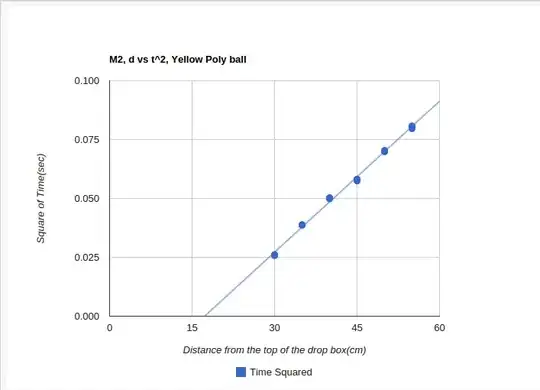
in Google Charts API
I am trying to do linear regression on this, i.e. trying to find the slope and the (y-) intercept of the trend line, and also the uncertainty in slope and uncertainty in intercept.
The Google Charts API already finds the slope and the intercept value when I draw the trend line, but I am not sure how to find the uncertainties.
I have been doing this using LINEST function in Excel, but I find this very cumbersome, since all my data are in Python.
So my question is, how can I find the two uncertainty values that I get in LINEST using Python?
I apologize for asking an elementary question like this.
I am pretty good at Python and Javascript, but I am very poor at regression analysis, so when I tried to look them up in documentations, because of the difficult terms, I got very confused.
I hope to use some well-known Python library, although it would be ideal if I could do this within Google Charts API.