Many questions exist already covering how to detect collisions between a line segment and a circle.
In my code, I am using Matlab's linecirc function, then comparing the intersection points it returns with the ends of my line segments, to check that the points are within the line (linecirc assumes an infinite line, which I don't have/want).
Copying and adding some sprintf calls to the linecirc function shows that it is calculating points as intended. These seem to be being lost by my function.
My code is below:
function cutCount = getCutCountHex(R_g, centre)
clf;
cutCount = 0;
% Generate a hex grid
Dg = R_g*2;
L_b = 62;
range = L_b*8;
dx = Dg*cosd(30);
dy = 3*R_g;
xMax = ceil(range/dx); yMax = ceil(range/dy);
d1 = @(xc, yc) [dx*xc dy*yc];
d2 = @(xc, yc) [dx*(xc+0.5) dy*(yc+0.5)];
centres = zeros((xMax*yMax),2);
count = 1;
for yc = 0:yMax-1
for xc = 0:xMax-1
centres(count,:) = d1(xc, yc);
count = count + 1;
centres(count, :) = d2(xc, yc);
count = count + 1;
end
end
for i=1:size(centres,1)
centres(i,:) = centres(i,:) - [xMax/2 * dx, yMax/2 * dy];
end
hold on
axis equal
% Get counter for intersected lines
[VertexX, VertexY] = voronoi(centres(:,1), centres(:,2));
numLines = size(VertexX, 2);
for lc = 1:numLines
segStartPt = [VertexX(1,lc) VertexY(1,lc)];
segEndPt = [VertexX(2,lc) VertexY(2,lc)];
slope = (segEndPt(2) - segStartPt(2))/(segEndPt(1) - segStartPt(1));
intercept = segEndPt(2) - (slope*segEndPt(1));
testSlope = isinf(slope);
if (testSlope(1)==1)
% Pass the x-axis intercept instead
intercept = segStartPt(1);
end
[xInterceptionPoints, yInterceptionPoints] = ...
linecirc(slope, intercept, centre(1), centre(2), L_b);
testArr = isnan(xInterceptionPoints);
if (testArr(1) == 0) % Line intersects. Line segment may not.
interceptionPoint1 = [xInterceptionPoints(1), yInterceptionPoints(1)];
interceptionPoint2 = [xInterceptionPoints(2), yInterceptionPoints(2)];
% Test if first intersection is on the line segment
p1OnSeg = onSeg(segStartPt, segEndPt, interceptionPoint1);
p2OnSeg = onSeg(segStartPt, segEndPt, interceptionPoint2);
if (p1OnSeg == 1)
cutCount = cutCount + 1;
scatter(interceptionPoint1(1), interceptionPoint1(2), 60, 'MarkerFaceColor', 'r', 'MarkerEdgeColor', 'k');
end
% Test if second intersection point is on the line segment
if (interceptionPoint1(1) ~= interceptionPoint2(1) || interceptionPoint1(2) ~= interceptionPoint2(2)) % Don't double count touching points
if (p2OnSeg == 1)
cutCount = cutCount + 1;
scatter(interceptionPoint2(1), interceptionPoint2(2), 60, 'MarkerFaceColor', 'r', 'MarkerEdgeColor', 'k');
end
end
end
end
% Plot circle
viscircles(centre, L_b, 'EdgeColor', 'b');
H = voronoi(centres(:,1), centres(:,2));
for i = 1:size(H)
set(H(i), 'Color', 'g');
end
end
function boolVal = onSeg(segStart, segEnd, testPoint)
bvX = isBetweenOrEq(segStart(1), segEnd(1), testPoint(1));
bvY = isBetweenOrEq(segStart(2), segEnd(2), testPoint(2));
if (bvX == 1 && bvY == 1)
boolVal = 1;
else
boolVal = 0;
end
end
function boolVal = isBetweenOrEq(end1, end2, test)
if ((test <= end1 && test >= end2) || (test >= end1 && test <= end2))
boolVal = 1;
else
boolVal = 0;
end
end
It creates a hexagonal grid, then calculates the number of crossings between a circle drawn with a fixed radius (62 in this case) and a specified centre.
The scatter calls show the locations that the function counts.
Implementing sprintf calls within the if(p1OnSeg == 1) block indicates that my function has chosen fictitious intersection points (although it then deals with them correctly)
if (interceptionPoint1(1) > -26 && interceptionPoint1(1) < -25)
sprintf('p1 = [%f, %f]. Vx = [%f, %f], Vy = [%f, %f].\nxint = [%f, %f], yint = [%f, %f]',...
interceptionPoint1(1), interceptionPoint1(2), VertexX(1,lc), VertexX(2,lc), VertexY(1,lc), VertexY(2,lc),...
xInterceptionPoints(1), xInterceptionPoints(2), yInterceptionPoints(1), yInterceptionPoints(2))
end
Outputs
p1 = [-25.980762, 0.000000]. Vx = [-25.980762, -25.980762], Vy = [-15.000000, 15.000000].
xint = [-25.980762, -25.980762], yint = [0.000000, 0.000000]
A picture shows the strange points.
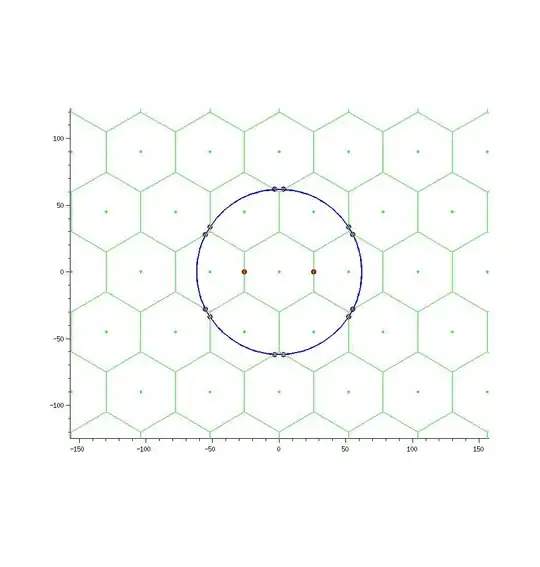
Sorry for the very long question but - why are these being detected. They don't lie on the circle (displaying values within a mylinecirc function detects the intersections at around (-25, 55) and (-25, -55) or so (as an infinite line would expect).
Moving the circle can remove these points, but sometimes this leads to other problems with detection. What's the deal?
Edit: Rotating my grid pattern created by [Vx, Vy] = voronoi(...) and then removing points with very large values (ie those going close to infinity etc) appears to have fixed this problem. The removal of 'large' value points seems to be necessary to avoid NaN values appearing in 'slope' and 'intercept'. My guess is this is related to a possible slight inclination due to rotation, coupled with then overflow of the expected intercept.
Example code added is below. I also edited in Jan de Gier's code, but that made no difference to the problem and so is not changed in the question code.
%Rotate slightly
RotAngle = 8;
RotMat = [cosd(RotAngle), -sind(RotAngle); sind(RotAngle), cosd(RotAngle)];
for i=1:size(centres,1)
centres(i,:) = centres(i,:) - [floor(xMax/2) * dx, floor(yMax/2) * dy]; %Translation
centres(i,:) = ( RotMat * centres(i,:)' ); %Rotation
end
% Get counter for intersected lines
[VertexX, VertexY] = voronoi(centres(:,1), centres(:,2));
% Filter vertices
numLines = size(VertexX, 2);
newVx = [];
newVy = [];
for lc = 1:numLines
testVec = [VertexX(:,lc) VertexY(:,lc)];
if ~any(abs(testVec) > range*1.5)
newVx = [newVx; VertexX(:,lc)'];
newVy = [newVy; VertexY(:,lc)'];
end
end
VertexX = newVx';
VertexY = newVy';
numLines = size(VertexX, 2);
Still appreciating answers or suggestions to clear up why this is/was occuring.
Example values that cause this are getCutCountHex(30, [0,0]) and ...(35, [0,0])