Haskell garbage collector

Question

I have a simple toy example that seems to disagree with the garbage collector on what data structures can be reclaimed (aka memory leak). I am not trying to come up with more memory efficient versions of this algorithm (a good collection of better algorithms is here: Haskell Wiki - Prime numbers, rather an explanation why the garbage collector is not identifying the old, out of scope and unused portions of the list to reclaim that memory.

The code is here:

import Data.List (foldl')

erat' :: (Integer, Bool) -> [(Integer,Integer)] -> [(Integer,Integer)]
erat' (c,b) ((x,y):xs)
    | c < x = (x,y) : erat' (c,b) xs
    | c == x = (x+y,y) : erat' (c,True) xs
    | c > x = (x+y,y) : erat' (c,b) xs
erat' (c,b) []
    | b = []
    | otherwise = [(c,c)]

erat :: [Integer] -> [(Integer,Integer)]
erat = foldl' (\a c -> erat' (c,False) a) []

primes :: Integer -> [Integer]
primes n = map snd $ erat [2..n]

In essence, calling primes with a positive integer will return a list of all prime numbers up to and including that number. A list of pairs of primes and their high water mark multiple is passed to erat', together with a pair including a candidate and a boolean (False for prime and True for non-prime). Every non-recursive call to erat' will pass a new list, and I would expect that the output would contain, at most, certain shared cells from the beginning of the list up to the point of the first change.

As soon as the modified cells in the list passed to erat' come out of scope, the memory should be flagged to be recovered, but as you can see when you try calling primes with a large enough number (1,000,000, for example), the memory utilization can quickly spike to tens of gigabytes.

Now, the question is: why is this happening? Shouldn't the generational garbage collector detect dereferenced list cells to reclaim them? And, shouldn't it be fairly easy for it to detect that they don't have references because:

a) nothing can have references from data structures older than itself; b) there cannot be newer references because those cells/fragments are not even part of a referenceable data structure anymore, since it came out of scope?

Of course, a mutable data structure would take care of this, but I feel like resorting to mutability in a case like this is dropping some of the theoretical principles for Haskell on the floor.

Thanks to the people that commented (particularly Carl), I modified the algorithm slightly to add strictness (and the optimization of starting crossing the square of the new prime, since lower multiples will be crossed by multiples of lower primes too).

This is the new version:

import Data.List (foldl')

erat' :: (Integer, Bool) -> [(Integer,Integer)] -> [(Integer,Integer)]
erat' (c,b) ((x,y):xs)
    | c < x = x `seq` (x,y) : erat' (c,b) xs
    | c == x = x `seq` (x+y,y) : erat' (c,True) xs
    | c > x = x `seq` (x+y,y) : erat' (c,b) xs
erat' (c,b) []
    | b = []
    | otherwise = [(c*c,c)] -- lower multiples would be covered by multiples of lower primes

erat :: [Integer] -> [(Integer,Integer)]
erat = foldl' (\a c -> erat' (c,False) a) []

primes :: Integer -> [Integer]
primes n = map snd $ erat [2..n]

The memory consumption seems to still be quite significant. Are there any other changes to this algorithm that could help reduce the total memory utilization?

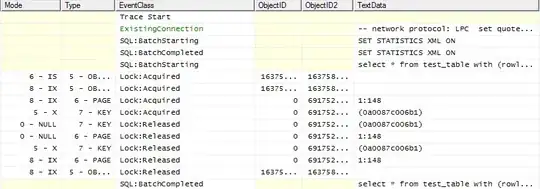
Since Will pointed out that I didn't provide full statistics, these are the numbers for a run of the updated version of primes listed just above, with 100000 as the parameter:

And after applying the changes that Will proposed, the memory usage is now down considerably. See, for example, on a run of primes for 100000 again:

And last, this is the final code after the proposed changes were incorporated:

import Data.List (foldl')

erat'' :: (Integer, Bool) -> [(Integer,Integer)] -> [(Integer,Integer)]
erat'' (c,b) ((x,y):xs)
    | c < x  = (x,  y) : if x==y*y then (if b then xs 
                                              else xs++[(c*c,c)])
                                   else erat'' (c,b)    xs 
    | c == x = (x+y,y) : if x==y*y then            xs 
                                   else erat'' (c,True) xs 
    | c > x  = (x+y,y) : erat'' (c,b)    xs 
erat'' (c,True)  [] = []
erat'' (c,False) [] = [(c*c,c)]


primes'' :: Integer -> [Integer]
primes'' n = map snd $ foldl' (\a c -> (if null a then 0 else 
        case last a of (x,y) -> y) `seq` erat'' (c,False) a) [] [2..n]

And finally a run for 1,000,000 to have a feeling for performance in this new version:

Answer 1

Assumption a) is false in the presence of laziness. And in fact, your code consists almost entirely of generating cons cells pointed to by older cons cells. erat' consumes a list element, then produces a (:) constructor pointing to a tuple and an unevaluated thunk which will perform a recursive call to erat'. Only when that thunk is later evaluated will the (:) list constructor actually point to its tail as a data structure. So yes, nearly every (:) you allocate in erat' is in fact pointing forward in time. (The only exception is the last one - [foo] is going to point to the pre-existing [] constructor when its (:) constructor is allocated.)

Assumption b) is nonsense in the presence of laziness. Scope determines visibility in Haskell, not lifetime. Lifetime depends on evaluation and reachability.

So what happens at runtime is that you build up pipeline of erat' calls in erat. Each one of them holds on to as much of its input as has been evaluated, slowly consuming it. The interesting part is that your code doesn't evaluate anything in advance - it seems like it should actually stream pretty well - except for the fact that the pipeline is too deep. The pipeline created is approximately n stages - this is (inefficient!) trial division, not the sieve of Eratosthenes. You should only be adding prime numbers to the pipeline, not every number.

Answer 2

breaking update: You should use

map snd $ foldl' (\a c -> (if null a then 0 else 
        case last a of (x,y) -> y) `seq` erat' (c,False) a) [] [2..n]

to force the list fully on each iteration. It will consume less memory and run faster.

The reason for the above is that foldl' only forces the accumulator to weak head normal form, and even using last a isn't enough, as it would be forced just to a pair (_,_), without forcing its constituents.

But when your erat' function is changed so that it stops scanning the interim list of primes and their multiples as soon as possible, and shares its tail whenever possible (as described below), it is faster without the forcing, even if using more memory.

---

Your (updated) code, edited a little for legibility:

g :: (Integer, Bool) -> [(Integer,Integer)] -> [(Integer,Integer)]
g (c,b) ((x,y):xs)
    | c < x  = (x,  y) : g (c,b)    xs  -- `c < x` forces the x already, 
    | c == x = (x+y,y) : g (c,True) xs  --              no need for `seq`
    | c > x  = (x+y,y) : g (c,b)    xs
g (c,True)  [] = []
g (c,False) [] = [(c*c,c)]

primes :: Integer -> [Integer]
primes n = map snd $ foldl' (\a c -> g (c,False) a) [] [2..n]

So, your primes n is actually a little like a right fold on the reversed [2..n] list. Writing h for flip $ foldl' (\a c -> g (c,False) a), it is

= map snd $ h [2..n] $ []
= map snd $ h [3..n] $ [(2*2,2)]
= map snd $ h [4..n] $ (4,2)  :(g (3,False) [])
= map snd $ h [5..n] $ (4+2,2):(g (4,True ) $ g (3,False) [])
= map snd $ h [6..n] $ (6,2)  :(g (5,False) $ g (4,True ) $ g (3,False) [])
....

The strictness of foldl' has limited effect here as the accumulator is forced only to the weak head normal form.

Folding with (\a c -> last a `seq` g (c,False) a) would give us

= map snd $ ... $ g (3,False) [(2*2,2)]
= map snd $ ... $ g (4,False) [(4,2),(3*3,3)]
= map snd $ ... $ g (5,False) [(4+2,2),(9,3)]
= map snd $ ... $ g (6,False) [(6,2),(9,3),(5*5,5)]
= map snd $ ... $ g (7,False) [(6+2,2),(9,3),(25,5)]
= map snd $ ... $ g (8,False) [(8,2),(9,3),(25,5),(7*7,7)]
= map snd $ ... $ g (9,False) [(8+2,2),(9,3),(25,5),(49,7)]
= map snd $ ... $ g (10,False) [(10,2),(9+3,3),(25,5),(49,7)]
= map snd $ ... $ g (11,False) [(10+2,2),(12,3),(25,5),(49,7)]
....
= map snd $ ... $ g (49,False) 
           [(48+2,2),(48+3,3),(50,5),(49,7),(121,11)...(2209,47)]
....

but all these changes will be pushed through to the list by the final print anyway, so the laziness is not the immediate problem here (it causes stack overflow for bigger inputs, but that's secondary here). The problem is that your erat' (renamed g above) eventually pushes each entry through the whole list needlessly, recreating the whole list for each candidate number. This is a very heavy memory usage pattern.

It should stop as early as possible, and share the list's tail whenever possible:

g :: (Integer, Bool) -> [(Integer,Integer)] -> [(Integer,Integer)]
g (c,b) ((x,y):xs)
    | c < x  = (x,  y) : if x==y*y then (if b then xs 
                                              else xs++[(c*c,c)])
                                   else g (c,b)    xs 
    | c == x = (x+y,y) : if x==y*y then            xs 
                                   else g (c,True) xs 
    | c > x  = (x+y,y) :                g (c,b)    xs 
g (c,True)  [] = []
g (c,False) [] = [(c*c,c)]

Compiled with -O2 and run standalone, it runs under ~ N^1.9 vs your original function's ~ N^{2.4..2.8..and rising}, producing primes up to N.

(of course a "normal" sieve of Eratosthenes should run at about ~ N^1.1, ideally, its theoretical time complexity being N log (log N)).