I'm looking for an algorithm to insert a new control point on a Bézier curve, without deforming.
Does anybody know a library or reference for Bézier algorithms (insertion, optimize, de Casteljau ...)?
I'm looking for an algorithm to insert a new control point on a Bézier curve, without deforming.
Does anybody know a library or reference for Bézier algorithms (insertion, optimize, de Casteljau ...)?
This is called the "knot insertion problem". For Bézier curves, the de Casteljau algorithm will give you the right answer. Here is the simple algorithm for a degree 3 Bézier.
Say you want to insert a knot at a fraction t of the parameter space inside the Bézier curve defined by P0, P1, P2, P3. Here's what you do:
P0_1 = (1-t)*P0 + t*P1
P1_2 = (1-t)*P1 + t*P2
P2_3 = (1-t)*P2 + t*P3
P01_12 = (1-t)*P0_1 + t*P1_2
P12_23 = (1-t)*P1_2 + t*P2_3
P0112_1223 = (1-t)*P01_12 + t*P12_23
Then your first Bézier will be defined by: P_0, P0_1, P01_12, P0112_1223; your second Bézier is defined by: P0112_1223, P12_23, P2_3, P3.
The geometrical interpretation is simple: you split each segment of the Bézier polygon at fraction t, then connect these split points in a new polygon and iterate. When you're left with 1 point, this point lies on the curve and the previous/next split points form the previous/next Bézier polygon. The same algorithm also works for higher degree Bézier curves.
Now it can get trickier if you want to insert the control point not at a specific value of t but at a specific location in space. Personally, what I would do here is simply a binary search for a value of t that falls close to the desired split point... But if performance is critical, you can probably find a faster analytic solution.
You could also take the mathematical approach.
A qubic Bézier curve with control points 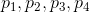 can be written as:
can be written as:
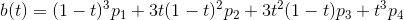
Its derivative w.r.t.  is
is

To limit the curve from 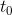 to
to  , you get new control points
, you get new control points 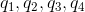 :
:

Substituting


We get

The first and last points of the sub-curve are the first and last new control points
And the tangent at those points is
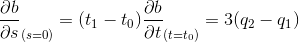
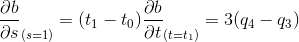
So


Adding this for completeness.
An open-source implementation of many Bézier path operations can be found inside GIMP source code, in gimpbezierstroke.c. For reference on inserting a new anchor, search for gimp_bezier_stroke_anchor_insert.