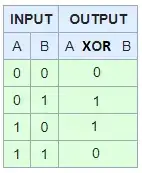
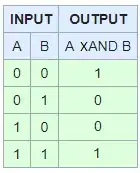
What are XAND and XOR

Question

What are XAND and XOR? Also is there an XNot

Answer 1

XOR is short for exclusive or. It is a logical, binary operator that requires that one of the two operands be true but not both.

So these statements are true:

TRUE XOR FALSE
FALSE XOR TRUE

And these statements are false:

FALSE XOR FALSE
TRUE XOR TRUE

There really isn't such a thing as an"exclusive and" (or XAND) since in theory it would have the same exact requirements as XOR. There also isn't an XNOT since NOT is a unary operator that negates its single operand (basically it just flips a boolean value to its opposite) and as such it cannot support any notion of exclusivity.

Answer 2

Guys, don´t scare the crap out of others (hey! just kidding), but it´s really all a question of equivalences and synonyms:

firstly:

"XAND" doesn´t exist logically, neither does "XNAND", however "XAND" is normally thought-up by a studious but confused initiating logic student.(wow!). It com from the thought that, if there´s a XOR(exclusive OR) it´s logical to exist a "XAND"("exclusive" AND). The rational suggestion would be an "IAND"("inclusive" AND), which isn´t used or recognised as well. So:

 XNOR <=> !XOR <=> EQV

And all this just discribes a unique operator, called the equivalency operator(<=>, EQV) so:

A  |  B  | A <=> B | A XAND B | A XNOR B | A !XOR B | ((NOT(A) AND B)AND(A AND NOT(B)))
---------------------------------------------------------------------------------------
T  |  T  |    T    |     T    |     T    |     T    |                T    
T  |  F  |    F    |     F    |     F    |     F    |                F    
F  |  T  |    F    |     F    |     F    |     F    |                F    
F  |  F  |    T    |     T    |     T    |     T    |                T    

And just a closing comment: The 'X' prefix is only possible if and only if the base operator isn´t unary. So, XNOR <=> NOT XOR <=/=> X NOR.

Peace.

Answer 3

XOR is Exclusive Or. It means "One of the two items being XOR'd is true, but not both of them."

TRUE XOR TRUE : FALSE
TRUE XOR FALSE : TRUE
FALSE XOR TRUE : TRUE
FALSE XOR FALSE: FALSE

Wikipedia's XOR Article

XAND I have not heard of.

Answer 4

In the book written by Charles Petzold titled "Code" he says there are 6 gates. There is the AND logical gate, the OR gate, the NOR gate, the NAND gate, and the XOR gate. He also mentions the 6th gate briefly calling it the "coincidence gate" and implies it's not used very often. He says it has the opposite output of a XOR gate because a XOR gate has the output of "false" when it has two true or two false sides of the equation and the only way for a XOR gate to have its output be true is for one of the sides of the equation to be true and the other to be false, it doesn't matter which. The coincidence is the exact opposite of this because with the coincidence gate if one is true and the other is false (doesn't matter which is which) then it will have its output be "false" in both those cases. And the way for a coincidence gate to have its output be "true" is for both sides to be either false or true. If both are false the coincidence gate will evaluate as true. If both are true then the coincidence gate will also output "true" in that case as well.

So in the cases where the XOR gate outputs "false", the coincidence gate will output "true". And in the cases where the XOR gate will output "true", the coincidence gate will output "false".

Answer 5

Hmm.. well I know about XOR (exclusive or) and NAND and NOR. These are logic gates and have their software analogs.

Essentially they behave like so:

XOR is true only when one of the two arguments is true, but not both.

F XOR F = F
F XOR T = T
T XOR F = T
T XOR T = F

NAND is true as long as both arguments are not true.

F NAND F = T
F NAND T = T
T NAND F = T
T NAND T = F

NOR is true only when neither argument is true.

F NOR F = T
F NOR T = F
T NOR F = F
T NOR T = F

Answer 6

This is what you are looking for: https://en.wikipedia.org/wiki/XNOR_gate

Here is the logic table:

A B   XOR XNOR
0 0   0   1 
0 1   1   0
1 0   1   0
1 1   0   1

XNOR sometimes is called XAND.

Answer 7

To add to this, since I was just dealing with it, if you are looking for an "equivalence gate" or a "coincedence gate" as your XAND, what you really have is just "equals".

If you think about it, given XOR from above:

F XOR F = F
F XOR T = T
T XOR F = T
T XOR T = F

And we expect XAND should be:

F XAND F = T
F XAND T = F
T XAND F = F
T XAND T = T

And isn't this exactly the same?

F == F = T
F == T = F
T == F = F
T == T = T

Answer 8

There is no such thing as Xand or Xnot. There is Nand, which is the opposite of and

TRUE and TRUE   : TRUE
TRUE and FALSE  : FALSE
FALSE and TRUE  : FALSE
FALSE and FALSE : FALSE


TRUE nand TRUE   : FALSE
TRUE nand FALSE  : TRUE
FALSE nand TRUE  : TRUE
FALSE nand FALSE : TRUE

Answer 9

There's a simple argument to see where the binary logic gates come from, using truth tables, which have come up already.

There are six that represent commutative operations, in which a op b == b op a. Each binary operator has an associated three column truth table that defines it. The first two columns can be fixed for the defining tables for all the operators.

Consider the third column. It's a sequence of four binary digits. There are sixteen combinations, but the constraint of commutativity effectively removes one row from the truth tables, so it's only eight. Two more get knocked off because all truths or all falses isn't a useful gate. These are the familiar or, and, and xor, plus their negations.

Answer 10

The truth tables on Wiki clarify http://en.wikipedia.org/wiki/Logic_gate There is no XAND, and that is the end of part 1 of the questions legitimacy. [The point is you can always make do without it.]

I personally have mistaken XNOT (which also doesn't exist) for NAND and NOR which are theoretically the only thing you need to make all the other gates link

I believe the confusion stems from the fact that you can use either NAND or NOR (to create everything else [but they are not needed together]), so it's thought of as one thing that's both NAND and NOR together, which basically leaves the mind to supplant the remaining name XNOT which isn't used so it's what I wrongly call XNOT meaning it's either NAND or NOR.

I suppose one could also wrongly in quick discussion try to use the XAND like I do XNOT, to refer to the "a single gate (copied in various arrangements) makes all other gates" logical reality.

Answer 11

XOR (not neither and not both) B'0110' is the inverse (dual) of IFF (if and only if) B'1001'.

Answer 12

In most cases you won't find an Xand, Xor, nor, nand Logical operator in programming, but fear not in most cases you can simulate it with the other operators.

Since you didn't state any particular language. I won't do any specific language either. For my examples we'll use the following variables.

A = 3
B = 5
C = 7

and for code I'll put it in the code tag to make it easier to see what I did, I'll also follow the logic through the process to show what the end result will be.

NAND

Also known as Not And, can easily be simulated by using a Not operator, (normally indicated as ! )

You can do the following

if(!((A>B) && (B<C)))

if (!(F&&T))
if(!(F))
If(T)

In our example above it will be true, since both sides were not true. Thus giving us the desired result

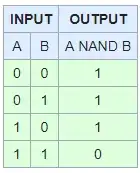
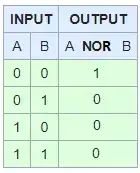
NOR

Also known as Not OR, just like NAND we can simulate it with the not operator.
if(!((A>B) || (B<C)))

if (!(F||T))
if(!(T))
if(F)

Again this will give us the desired outcomes

XOR

Xor or Exlcusive OR only will be true when one is TRUE but the Other is FALSE

If (!(A > C && B > A) && (A > C || B > A) )

If (!(F && T) && (F || T) )
If (!(F) && (T) )
If (T && T )
If (T)

So that is an example of it working for just 1 or the other being true, I'll show if both are true it will be false.

If ( !(A < C && B > A) && (A < C || B > A) )

If ( !(T && T) && (T ||T) )
If ( !(T) && (T) )
If ( F && T )
If (F)

And both false

If (!(A > C && B < A) && (A > C || B < A) )

If (!(F && F) && (F || F) )
If (!(F) && (F) )
If (T && F )
If (F)

And the picture to help

XAND

And finally our Exclusive And, this will only return true if both are sides are false, or if both are true. Of course You could just call this a Not XOR (NXOR)

Both True If ( (A < C && B > A) || !(A < C || B > A) )

If ((T&&T) || !(T||T))
IF (T || !T)
If (T || F)
IF (T)

Both False If ( (A > C && B < A) || !(A > C || B < A) )

If ( (F && F) || !(F ||F))
If ( F || !F)
If ( F || T)
If (T)

And lastly 1 true and the other one false. If ((A > C && B > A) || !(A > C || B > A) )

If ((F && T) || ! (F || T) )
If (F||!(T))
If (F||F)
If (F)

Or if you want to go the NXOR route...
If (!(!(A > C && B > A) && (A > C || B > A)))

If (!(!(F && T) && (F || T)) )
If (!(!(F) && (T)) )
If (!(T && T) )
If (!(T))
If (F)

Of course everyone else's solutions probably state this as well, I am putting my own answer in here because the top answer didn't seem to understand that not all languages support XOR or XAND for example C uses ^ for XOR and XAND isn't even supported.

So I provided some examples of how to simulate it with the basic operators in the event your language doesn't support XOR or XAND as their own operators like Php if ($a XOR $B).

As for Xnot what is that? Exclusive not? so not not? I don't know how that would look in a logic gate, I think it doesn't exist. Since Not just inverts the output from a 1 to a 0 and 0 to a 1.

Anyway hope that helps.

Answer 13

The XOR definition is well known to be the odd-parity function. For two inputs:

A XOR B = (A AND NOT B) OR (B AND NOT A)

The complement of XOR is XNOR

A XNOR B = (A AND B) OR (NOT A AND NOT B)

Henceforth, the normal two-input XAND defined as

A XAND B = A AND NOT B

The complement is XNAND:

A XNAND B = B OR NOT A

A nice result from this XAND definition is that any dual-input binary function can be expressed concisely using no more than one logical function or gate.

            +---+---+---+---+
   If A is: | 1 | 0 | 1 | 0 |
  and B is: | 1 | 1 | 0 | 0 |
            +---+---+---+---+
    Then:        yields:     
+-----------+---+---+---+---+
| FALSE     | 0 | 0 | 0 | 0 |
| A NOR B   | 0 | 0 | 0 | 1 |
| A XAND B  | 0 | 0 | 1 | 0 |
| NOT B     | 0 | 0 | 1 | 1 |
| B XAND A  | 0 | 1 | 0 | 0 |
| NOT A     | 0 | 1 | 0 | 1 |
| A XOR B   | 0 | 1 | 1 | 0 |
| A NAND B  | 0 | 1 | 1 | 1 |
| A AND B   | 1 | 0 | 0 | 0 |
| A XNOR B  | 1 | 0 | 0 | 1 |
| A         | 1 | 0 | 1 | 0 |
| B XNAND A | 1 | 0 | 1 | 1 |
| B         | 1 | 1 | 0 | 0 |
| A XNAND B | 1 | 1 | 0 | 1 |
| A OR B    | 1 | 1 | 1 | 0 |
| TRUE      | 1 | 1 | 1 | 1 |
+-----------+---+---+---+---+

Note that XAND and XNAND lack reflexivity.

This XNAND definition is extensible if we add numbered kinds of exclusive-ANDs to correspond to their corresponding minterms. Then XAND must have ceil(lg(n)) or more inputs, with the unused msbs all zeroes. The normal kind of XAND is written without a number unless used in the context of other kinds.

The various kinds of XAND or XNAND gates are useful for decoding.

XOR is also extensible to any number of bits. The result is one if the number of ones is odd, and zero if even. If you complement any input or output bit of an XOR, the function becomes XNOR, and vice versa.

I have seen no definition for XNOT, I will propose a definition:

Let it to relate to high-impedance (Z, no signal, or perhaps null valued Boolean type Object).

0xnot 0 = Z
0xnot 1 = Z
1xnot 0 = 1
1xnot 1 = 0

Answer 14

Have a look

x   y      A    B   C   D   E   F   G   H   I   J   K   L   M   N

·   ·      T    ·   T   ·   T   ·   T   ·   T   ·   T   ·   T   ·
·   T      ·    T   T   ·   ·   T   T   ·   ·   T   T   ·   ·   T
T   ·      ·    ·   ·   T   T   T   T   ·   ·   ·   ·   T   T   T
T   T      ·    ·   ·   ·   ·   ·   ·   T   T   T   T   T   T   T

A) !(x OR y)    
B) !(x) AND y   
C) !(x) 
D) x AND !(y)   
E) !(y) 
F) x XOR y  
G) !(x AND y)   
H) x AND y  
I) !(x XOR y)   
J) y    
K) !(x) OR y    
L) x    
M) x OR !(y)    
N) x OR y

Answer 15

XOR behaves like Austin explained, as an exclusive OR, either A or B but not both and neither yields false.

There are 16 possible logical operators for two inputs since the truth table consists of 4 combinations there are 16 possible ways to arrange two boolean parameters and the corresponding output.

They all have names according to this wikipedia article

Answer 16

OMG, a XAND gate does exist. My dad is taking a technological class for a job and there IS an XAND gate. People are saying that both OR and AND are complete opposites, so they expand that to the exclusive-gate logic:

XOR: One or another, but not both.

Xand: One and another, but not both.

This is incorrect. If you're going to change from XOR to XAND, you have to flip every instance of 'AND' and 'OR':

XOR: One or another, but not both.

XAND: One and another, but not one.

So, XAND is true when and only when both inputs are equal, either if the inputs are 0/0 or 1/1

Answer 17

First comes the logic, then the name, possibly patterned on previous naming.

Thus 0+0=0; 0+1=1; 1+0=1; 1+1=1 - for some reason this is called OR.

Then 0-0=0; 0-1=1; 1-0=1; 1-1=0 - it looks like OR except ... let's call it XOR.

Also 0*0=0; 0*1=0; 1*0=0; 1*1=1 - for some reason this is called AND.

Then 0~0=0; 0~1=0; 1~0=0; 1~1=0 - it looks like AND except ... let's call it XAND.

Answer 18

Logically there are 8 gates OR XOR AND and XAND plus their negations NOR XNOR NAND and XNAND. XOR is equivalent to XNAND and XAND is equivalent to XNOR. A OR B = NOTA NAND NOTB A AND B = NOTA NOR NOTB The Sheffer bar NAND is more consistently written as an up arrow to complement the Peirce down arrow NOR. That’s everything in a nutshell.