This question is similar to Fit a non-linear function to data/observations with pyMCMC/pyMC, in that I'm trying to do nonlinear regression using PyMC.
However, I was wondering if anyone knew how to make my observed variable follow a non-normal distribution (i.e., T distribution) using PyMC. I know they include T distributions, but I wasn't sure how to include these as my observed variable.
Here's a quick demonstration using some faked-up data of where I'm running into issues: I'd like to use an output distribution that protects against some of the clearly outlier data points.
import numpy as np
import pymc as pm
import matplotlib.pyplot as plt
# For reproducibility
np.random.seed(1234)
x = np.linspace(0, 10*np.pi, num=150)
# Set real parameters for the sinusoid
true_freq = 0.9
true_logamp = 1.2
true_decay = 0.12
true_phase = np.pi/4
# Simulate the true trajectory
y_real = (np.exp(true_logamp - true_decay*x) *
np.cos(true_freq*x + true_phase))
# Add some noise
y_err = y_real + 0.05*y_real.max()*np.random.randn(len(x))
# Add some outliers
num_outliers = 10
outlier_locs = np.random.randint(0, len(x), num_outliers)
y_err[outlier_locs] += (10 * y_real.max() *
(np.random.rand(num_outliers)))
# Bayesian Regression
def model(x, y, p0):
log_amp = pm.Normal('log_amp', mu=np.log(p0['amplitude']),
tau=1/(np.log(p0['amplitude'])))
decay = pm.Normal('decay', mu=p0['decay'],
tau=1/(p0['decay']))
period = pm.TruncatedNormal('period', mu=p0['period'],
tau=1/(p0['period']),
a=1/(0.5/(np.median(np.diff(x)))),
b=x.max() - x.min())
phase = pm.VonMises('phase', mu=p0['phase'], kappa=1.)
obs_tau = pm.Gamma('obs_tau', 0.1, 0.1)
@pm.deterministic(plot=False)
def decaying_sinusoid(x=x, log_amp=log_amp, decay=decay,
period=period, phase=phase):
return (np.exp(log_amp - decay*x) *
np.cos((2*np.pi/period)*x + phase))
obs = pm.Normal('obs', mu=decaying_sinusoid, tau=obs_tau, value=y,
observed=True)
return locals()
p0 = {
'amplitude' : 2.30185,
'decay' : 0.06697,
'period' : 7.11672,
'phase' : 0.93055,
}
MDL = pm.MCMC(model(x, y_err, p0))
MDL.sample(20000, 10000, 1)
# Plot fit
y_min = MDL.stats()['decaying_sinusoid']['quantiles'][2.5]
y_max = MDL.stats()['decaying_sinusoid']['quantiles'][97.5]
y_fit = MDL.stats()['decaying_sinusoid']['mean']
plt.plot(x, y_err, '.', label='Data')
plt.plot(x, y_fit, label='Fit')
plt.plot(x, y_real, label='True')
plt.fill_between(x, y_min, y_max, color='0.5', alpha=0.5)
plt.legend()
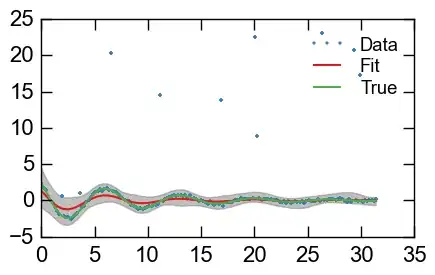
Thanks!!