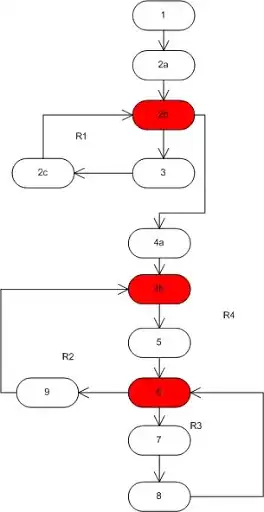
insertion_procedure (int a[], int p [], int N)
{
int i,j,k;
for (i=0; i<=N; i++) p[i] = i;
for (i=2; i<=N; i++)
{
k = p[i];
j = 1;
while (a[p[j-1]] > a[k]) {p[j] = p[j-1]; j--}
p[j] = k;
}
}
I have to find cyclomatic complexity for this code and then suggest some white box test cases and black box test cases. But I am having trouble making a CFG for the code.
Would appreciate some help on test cases as well.