7

I am looking to remove outliers before I apply a model. I am using a Loess curve to delimit the trend line and have set outlier limits. I would like to remove the rows that are outside the defined limits. Besides doing this with a custom function that takes each point one at a time and checks the local Loess slope etc... is there an easier way?

Loess trend line with limits (1.2)

# Code generating image above
scatter.smooth( idam$T_d, idam$T_x10d)
loessline <- loess.smooth( idam$T_d, idam$T_x10d)
lines(loessline$x, loessline$y, lwd=3)
lines(loessline$x, loessline$y*1.2, lwd=3, col='red')
lines(loessline$x, loessline$y/1.2, lwd=3, col='red')
Cyrille
  • 3,427
  • 1
  • 30
  • 32
  • Be cautious. If physics doesn't give a good reason to throw away data, then you might be doing a bad thing by throwing out good but less easily handled data. – EngrStudent Oct 05 '17 at 15:00

3 Answers3

8

You can use approxfun

Here is an example with "outliers"

plot(wt ~ mpg, data = mtcars)
lo <- loess.smooth(mtcars$mpg, mtcars$wt)
lines(lo$x, lo$y, lwd = 3)
lines(lo$x, lo$y * 1.2, lwd = 3, col = 2)
lines(lo$x, lo$y / 1.2, lwd = 3, col = 2)

enter image description here

approxfun returns a function using the observed x-values that we can use to interpolate a set of new y-values.

Then, you can set a threshold for calling a point an outlier; here I am using 1.2 * y as in the original question to identify the extreme observations.

f1 <- approxfun(lo$x, lo$y * 1.2)
(wh1 <- which(mtcars$wt > f1(mtcars$mpg)))
# [1]  8 17 18

f2 <- approxfun(lo$x, lo$y / 1.2)
(wh2 <- which(mtcars$wt < f2(mtcars$mpg)))
# [1] 28

## identify points to exclude
mt <- mtcars[c(wh1, wh2), ]
points(mt$mpg, mt$wt, pch = 4, col = 2, cex = 2)

enter image description here

## plot without points
plot(wt ~ mpg, data = mt2 <- mtcars[-c(wh1, wh2), ])
lo <- loess.smooth(mt2$mpg, mt2$wt)
lines(lo$x, lo$y, lwd = 3)
lines(lo$x, lo$y * 1.2, lwd = 3, col = 2)
lines(lo$x, lo$y / 1.2, lwd = 3, col = 2)

enter image description here

Since there are a couple steps here, you could package this into a function to make things a little easier:

par(mfrow = c(2,2))
with(mtcars, {
  plot_lo(mpg, wt)
  plot_lo(mpg, wt, limits = c(1 / 1.5, 1.5))
  dd <<- plot_lo(mpg, wt, limits = c(1 / 1.2, 1.2))
  plot_lo(mpg, wt, pch = 16, las = 1, tcl = .5, bty = 'l')
})

str(dd)
# List of 2
# $ x: num [1:28] 21 21 22.8 21.4 18.7 18.1 14.3 22.8 19.2 17.8 ...
# $ y: num [1:28] 2.62 2.88 2.32 3.21 3.44 ...

enter image description here

plot_lo <- function(x, y, limits = c(-Inf, Inf), ...) {
  lo <- loess.smooth(x, y)
  fx <- approxfun(lo$x, lo$y * limits[1L])
  fy <- approxfun(lo$x, lo$y * limits[2L])

  idx <- which(y < fx(x) | y > fy(x))
  if (length(idx)) {
    x  <- x[-idx]
    y  <- y[-idx]
    lo <- loess.smooth(x, y)
  }

  op <- par(..., no.readonly = TRUE)
  on.exit(par(op))

  plot(x, y)
  lines(lo$x, lo$y, lwd = 3)
  lines(lo$x, lo$y * limits[1L], lwd = 3, col = 2L)
  lines(lo$x, lo$y * limits[2L], lwd = 3, col = 2L)

  invisible(list(x = x, y = y))
}
rawr
  • 20,481
  • 4
  • 44
  • 78
  • Isn't the x1.2 factor a little bit arbitrary here? – user2398029 Jan 19 '16 at 19:16
  • @user2398029 are you asking me or the op? – rawr Jan 19 '16 at 19:18
  • I just noticed the OP had that factor in his question, so I guess the answer does follow along. Isn't there a way to set this factor in non-arbitrary fashion? – user2398029 Jan 19 '16 at 19:20
  • @user2398029 I think the `lo$y * limits[1]` could be replaced with anything, using a `quantile` or `sd` on the y-values instead of a simple scaling. the nice thing about statistics is that you can do anything! so long as you can justify it – rawr Jan 19 '16 at 19:26
8

Detecting outliers could be done with help of DBSCAN R package, well-known algorithm used for cluster identification (see WIKIPEDIA for more details ).

This function has three important inputs:

  • x: your data (only numeric value)
  • eps: the target maximal distance
  • minPts: number of minimal points to consider them as a cluster

Evaluating eps can be done with help of knndist(...) and knndistplot(...) functions:

  • knndistplot will plot the eps values on your data set for a given k (i.e. minPts) ==> you could visually select an effective eps value (generally in the knee curve part)
  • knndist will evaluate eps values and return them in matrix from. the k input will generate 1:1:k valuations and you could use the result for determining programatically the accurate eps & k values

Next you have just to use dbscan(yourdata, eps, k) for getting a dbscan object with following components:

  • eps: the eps used for calculations
  • minPts: the minimal number of points for identifying a cluster
  • cluster: an integer vector identifying points which belongs to a cluster (=1) or not (=0). The last ones correspond to the outliers you want to eliminate.

Please note the following limitations on dbscan:

  • dbscan use euclidean distance and so it is submitted to "Curse of Dimensions". This can be avoided with use of PCA
  • dbscan eliminates superposed points which might generate unidentified points. This can be solved either by merging the results with your data with a left outer join or by using jitter(...) function which adds noise to your data. According to the data you displayed, I think it could be the case for your data

knowing this limitations, dbscan package offers two alternative methods : LOF and OPTICS (an extension of DBSCAN)

Edit on 25 Jabuary 2016

Following @rawr answer, I'm giving an example based on mtcars dataset to show how to use dbscan for identifying outliers. Please note that my example will use the excellent data.table package instead of the classical data.frame.

First, I start to replicate rawr's approach for illustrating the use of data.table

require(data.table)
require(ggplot2)
require(dbscan)
data(mtcars)
dt_mtcars <- as.data.table(mtcars)

# based on rawr's approach
plot(wt~mpg, data=dt_mtcars)
lo <- loess.smooth(dt_mtcars[,mpg], dt_mtcars[,wt])
lines(lo$x,lo$y, lwd=3)
lines(lo$x,lo$y * 1.2, lwd=3 , col=2 )
lines(lo$x,lo$y / 1.2, lwd=3 , col=2 )

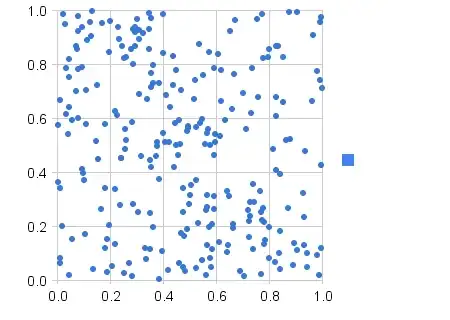
enter image description here

Thereby, we can assess that we get the same results independently of underlying support.

Second, the following code illustrate the DBSCAN approach which starts with determining eps and k, the necessary number of points to identifying a cluster:

res_knn = kNNdist( dt_mtcars[, .(wt, mpg)] , k = 10)
dim_knn = dim(res_knn)
x_knn =  seq(1, dim_knn[1])
ggplot() + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 1])  , col = 1 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 2])  , col = 2 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 3])  , col = 3 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 4])  , col = 4 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 5])  , col = 5 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 6])  , col = 6 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 7])  , col = 7 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 8])  , col = 8 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 9])  , col = 9 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 10]) , col = 10 ) )  +
   xlab('sorted results') + 
   ylab('kNN distance')

The results are plotted in following graphic:

enter image description here

It shows that the calculated kNN distance is sensitive to the factor k however the accurate eps value for segregating outliers is located in the knee part of the curves ==> suitable eps is located between 2 and 4. This is a visual assessment which could be automatized with appropriate search algorithms (for instance, see this link). Regarding k, a tradeoff must be defined, knowing the lower k is, the less stringent results are.

In next part, we will parametrize dbscan with eps = 3 (based on visual estimation) and k = 4 for having slight stringent results. We will plot these results with help of rawr's code:

eps = 3
k = 4
res_dbscan = dbscan( dt_mtcars[, .(wt, mpg)] , eps , k )
plot(wt~mpg, data=dt_mtcars, col = res_dbscan$cluster)
lo <- loess.smooth(dt_mtcars[res_dbscan$cluster>0,mpg], dt_mtcars[res_dbscan$cluster>0,wt])
lines(lo$x,lo$y, lwd=3)
lines(lo$x,lo$y * 1.2, lwd=3 , col=2 )
lines(lo$x,lo$y / 1.2, lwd=3 , col=2 )

enter image description here

we got this figure where we can assess that we got different results from rawr's approach, where the points located in mpg = [10,13] are considered as outliers.

These results could considered as odd comparing to rawr's solution, which works under the assumptions of having bivariate data (Y ~ X). However mtcars is a multidimensional dataset where relationship between variables might be (or not) linear... To assess this point, we could scatterplot this dataset, filtered on numerical values for instance 

pairs(dt_mtcars[, .(mpg, disp, hp, drat, wt, qsec)])

enter image description here

If we focus only on the result wt ~ mpg, we might think it is an anti-linear relationship at first look. But with other plotted relationships, this might be not the case and finding outliers in N-Dim environment is a bit trickier. Indeed one point might be considered as outlier when projected in particular 2D comparison... but inversely if we add a new comparison dimension. Indeed we might have collinearity which could be identified and so strengthen the cluster relationship or not.

My friends, I agree it's a lot of if and in order to illustrate this situation, we will proceed to a dbscan analysis on numeric values of mtcars.

So I will replicate the process presented earlier and let's start with the kNN distance analysis:

res_knn = kNNdist( dt_mtcars[, .(mpg, disp, hp, drat, wt, qsec)] , k = 10)
dim_knn = dim(res_knn)
x_knn =  seq(1, dim_knn[1])
ggplot() + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 1])  , col = 1 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 2])  , col = 2 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 3])  , col = 3 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 4])  , col = 4 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 5])  , col = 5 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 6])  , col = 6 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 7])  , col = 7 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 8])  , col = 8 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 9])  , col = 9 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 10]) , col = 10 ) )  +
    xlab('sorted results') + 
    ylab('kNN distance')

sorted kNN distances

Comparatively to the analysis produced on wt ~ mpg, we can see that kNNdist(...) produce far more important kNN distance (until 200 with k = 10 for instance). However we still have the knee part which help us to estimate a suitable eps value.

In next part, we will use eps = 75 and k = 5 and

# optimal eps value is between 40 (k=1) and 130 (k=10)
eps = 75
k = 5
res_dbscan = dbscan( dt_mtcars[, .(mpg, disp, hp, drat, wt, qsec)] , eps , k )
pairs(dt_mtcars[, .(mpg, disp, hp, drat, wt, qsec)] , col = res_dbscan$cluster+2L)

enter image description here

Thereby the scatterplot of this analysis highlights that identifying outliers could be tricky in N-Dim environment, due to complex relationships between variables. But please note that in most of cases, the outliers are located in a corner part of the 2D projection, which strengthen the results obtained with wt ~ mpg

Community
  • 1
  • 1
Bruno Sarrant
  • 309
  • 2
  • 7
  • How would one apply a clustering algorithm to time series data? – user2398029 Jan 19 '16 at 19:15
  • @user2398029: time series data could be consider as numeric values as well. For instance, Excel or Matlab define a reference time point and use date format as an alias of a "YYYY-MM-DD" format. Thus you're able to switch from a string value to a numeric value. Another way to integrate time series data is the presence of seasonality over a periode, so you can consider time data as a stacking factor. You could also convert time data as factor by distinguishing year, month, day and so on. – Bruno Sarrant Jan 20 '16 at 10:15
  • Of course... I'm asking how to apply a *clustering* algorithm to data that does not form clusters. – user2398029 Jan 20 '16 at 19:54
  • Thanks for the clarification and the point is : how could you assess that your data don't form a cluster, even if you have a 2-dimensional case (Value vs. Time)? For instance, you can have seasonal effects which aggregates results at certain time points ... For sure, in case you have a strict linear effect, using DBSCAN could be useless in 2D case... but if you have multidimensional data, some correlations might occur and hidden when reflecting your data in a representation with less dimensions. I'm working on an edit of my answer, based on "mtcars" dataset for highlighting this point – Bruno Sarrant Jan 21 '16 at 10:52
0

My suggestion is to go have a look at the outliers package. This package allows for identification before analysis happens. This is a very SIMPLE example:

library(outliers)
series<-c(runif(100,1,2),1000)
round(scores(series,prob=1,type="chisq"),3)

With this function, a multitude of test can be performed and you can set a probability level of being an outlier, that you are comfortable with.

series<-series[which(series<0.95),]
Hanjo Odendaal
  • 1,395
  • 2
  • 13
  • 32