Not knowledgeable enough in Python to answer this in your requested language, but in C/C++, given the parameters of your question, I'd convert the zeros and ones to bits and push them onto the least significant bits of an uint64_t. This will allow you to compare all 55 bits in one fell swoop - 1 clock.
Wickedly fast, and the whole thing will fit in on-chip caches (209,880 bytes). Hardware support for shifting all 55 list members right simultaneously is available only in a CPU's registers. The same goes for comparing all 55 members simultaneously. This allows for a 1-for-1 mapping of the problem to a software solution. (and using the SIMD/SSE 256 bit registers, up to 256 members if needed) As a result the code is immediately obvious to the reader.
You might be able to implement this in Python, I just don't know it well enough to know if that's possible or what the performance might be.
After sleeping on it a few things became obvious, and all for the better.
1.) It's so easy to spin the circularly linked list using bits that Dali's very clever trick isn't necessary. Inside a 64-bit register standard bit shifting will accomplish the rotation very simply, and in an attempt to make this all more Python friendly, by using arithmetic instead of bit ops.
2.) Bit shifting can be accomplished easily using divide by 2.
3.) Checking the end of the list for 0 or 1 can be easily done by modulo 2.
4.) "Moving" a 0 to the head of the list from the tail can be done by dividing by 2. This because if the zero were actually moved it would make the 55th bit false, which it already is by doing absolutely nothing.
5.) "Moving" a 1 to the head of the list from the tail can be done by dividing by 2 and adding 18,014,398,509,481,984 - which is the value created by marking the 55th bit true and all the rest false.
6.) If a comparison of the anchor and composed uint64_t is TRUE after any given rotation, break and return TRUE.
I would convert the entire array of lists into an array of uint64_ts right up front to avoid having to do the conversion repeatedly.
After spending a few hours trying to optimize the code, studying the assembly language I was able to shave 20% off the runtime. I should add that the O/S and MSVC compiler got updated mid-day yesterday as well. For whatever reason/s, the quality of the code the C compiler produced improved dramatically after the update (11/15/2014). Run-time is now ~ 70 clocks, 17 nanoseconds to compose and compare an anchor ring with all 55 turns of a test ring and NxN of all rings against all others is done in 12.5 seconds.
This code is so tight all but 4 registers are sitting around doing nothing 99% of the time. The assembly language matches the C code almost line for line. Very easy to read and understand. A great assembly project if someone were teaching themselves that.
Hardware is Hazwell i7, MSVC 64-bit, full optimizations.
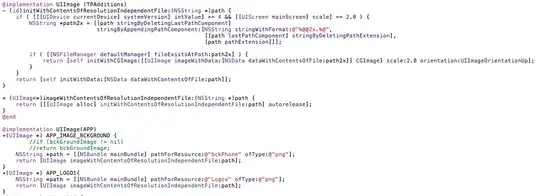
#include "stdafx.h"
#include "stdafx.h"
#include <string>
#include <memory>
#include <stdio.h>
#include <time.h>
const uint8_t LIST_LENGTH = 55; // uint_8 supports full witdth of SIMD and AVX2
// max left shifts is 32, so must use right shifts to create head_bit
const uint64_t head_bit = (0x8000000000000000 >> (64 - LIST_LENGTH));
const uint64_t CPU_FREQ = 3840000000; // turbo-mode clock freq of my i7 chip
const uint64_t LOOP_KNT = 688275225; // 26235^2 // 1000000000;
// ----------------------------------------------------------------------------
__inline uint8_t is_circular_identical(const uint64_t anchor_ring, uint64_t test_ring)
{
// By trial and error, try to synch 2 circular lists by holding one constant
// and turning the other 0 to LIST_LENGTH positions. Return compare count.
// Return the number of tries which aligned the circularly identical rings,
// where any non-zero value is treated as a bool TRUE. Return a zero/FALSE,
// if all tries failed to find a sequence match.
// If anchor_ring and test_ring are equal to start with, return one.
for (uint8_t i = LIST_LENGTH; i; i--)
{
// This function could be made bool, returning TRUE or FALSE, but
// as a debugging tool, knowing the try_knt that got a match is nice.
if (anchor_ring == test_ring) { // test all 55 list members simultaneously
return (LIST_LENGTH +1) - i;
}
if (test_ring % 2) { // ring's tail is 1 ?
test_ring /= 2; // right-shift 1 bit
// if the ring tail was 1, set head to 1 to simulate wrapping
test_ring += head_bit;
} else { // ring's tail must be 0
test_ring /= 2; // right-shift 1 bit
// if the ring tail was 0, doing nothing leaves head a 0
}
}
// if we got here, they can't be circularly identical
return 0;
}
// ----------------------------------------------------------------------------
int main(void) {
time_t start = clock();
uint64_t anchor, test_ring, i, milliseconds;
uint8_t try_knt;
anchor = 31525197391593472; // bits 55,54,53 set true, all others false
// Anchor right-shifted LIST_LENGTH/2 represents the average search turns
test_ring = anchor >> (1 + (LIST_LENGTH / 2)); // 117440512;
printf("\n\nRunning benchmarks for %llu loops.", LOOP_KNT);
start = clock();
for (i = LOOP_KNT; i; i--) {
try_knt = is_circular_identical(anchor, test_ring);
// The shifting of test_ring below is a test fixture to prevent the
// optimizer from optimizing the loop away and returning instantly
if (i % 2) {
test_ring /= 2;
} else {
test_ring *= 2;
}
}
milliseconds = (uint64_t)(clock() - start);
printf("\nET for is_circular_identical was %f milliseconds."
"\n\tLast try_knt was %u for test_ring list %llu",
(double)milliseconds, try_knt, test_ring);
printf("\nConsuming %7.1f clocks per list.\n",
(double)((milliseconds * (CPU_FREQ / 1000)) / (uint64_t)LOOP_KNT));
getchar();
return 0;
}