YinYang puzzle is written in Scheme. I assume you know the basic syntax of Scheme.
But I assume you don't know let* or call-with-current-continuation, I will explain these two keywords.
Explain let*
If you already know that, you can skip to Explain call-with-current-continuation
let*, which looks like let, acts like let, but will evaluate its defined variables(the (yin ...) and (yang ...)) one by one and eagerly. That means, it will first evaluate yin, and than yang.
You can read more in here:
Using Let in Scheme
Explain call-with-current-continuation
If you already know that, you can skip to Yin-Yang puzzle.
It's a little bit hard to explain call-with-current-continuation. So I will use a metaphor to explain it.
Image a wizard who knew a spell, which was call-with-current-continuation. Once he cast the spell, he would create a new universe, and send him-self to it. But he could do nothing in the new universe but waiting for someone calling his name. Once been called, the wizard would return to the original universe, having the poor guy -- 'someone' -- in hand, and go on his wizard life. If not been called, when the new universe ended, the wizard also returned to the original universe.
Ok, let's be more technical.
call-with-current-continuation is a function which accept a function as parameter. Once you call call-with-current-continuation with a function F, it will pack the current running environment, which is called current-continuation, as a parameter C, and send it to function F, and execute F. So the whole program becomes (F C). Or being more JavaScript: F(C);. C acts like a function. If C is not called in F, then it is an ordinary program, when F returns, call-with-current-continuation has a value as F's return value. But if C is called with a parameter V, it will change the whole program again. The program changes back to a state when call-with-current-continuation been called. But now call-with-current-continuation yields a value, which is V. And the program continues.
Let's take an example.
(define (f return)
(return 2)
3)
(display (f whatever)) ;; 3
(display (call-with-current-continuation f)) ;; 2
(display (call-with-current-continuation (lambda (x) 4))) ;; 4
The first display output 3, of cause.
But the second display output 2. Why?
Let's dive into it.
When evaluating (display (call-with-current-continuation f)), it will first evaluate (call-with-current-continuation f). We know that it will change the whole program to
(f C)
Considering the definition for f, it has a (return 2). We must evaluate (C 2). That's when the continuation being called. So it change the whole program back to
(display (call-with-current-continuation f))
But now, call-with-current-continuation has value 2. So the program becomes:
(display 2)
Yin-Yang puzzle
Let's look at the puzzle.
(let* ((yin
((lambda (cc) (display #\@) cc) (call-with-current-continuation (lambda (c) c))))
(yang
((lambda (cc) (display #\*) cc) (call-with-current-continuation (lambda (c) c)))))
(yin yang))
Let's make it more readable.
(define (id c) c)
(define (f cc) (display #\@) cc)
(define (g cc) (display #\*) cc)
(let* ((yin
(f (call-with-current-continuation id)))
(yang
(g (call-with-current-continuation id))))
(yin yang))
Let's run the program in our brain.
Round 0
let* make us to evaluate yin first. yin is
(f (call-with-current-continuation id))
So we evaluate (call-with-current-continuation id) first. It packs the current environment, which we call it C_0 to distinguish with other continuation in the time-line, and it enters a whole new universe: id. But id just returns C_0.
We should Remember what C_0 is. C_0 is a program like this:
(let* ((yin
(f ###))
(yang
(g (call-with-current-continuation id))))
(yin yang))
### is a placeholder, which in the future will be filled by the value that C_0 takes back.
But id just returns C_0. It doesn't call C_0. If it calls, we will enter C_0's universe. But it didn't, so we continue to evaluate yin.
(f C_0) ;; yields C_0
f is a function like id, but it has a side effect -- outputting @.
So the program output @ and let yin to be C_0. Now the program becomes
(let* ((yin C_0)
(yang
(g (call-with-current-continuation id))))
(yin yang))
After yin evaluated, we start to evaluate yang. yang is
(g (call-with-current-continuation id))
call-with-current-continuation here create another continuation, named C_1. C_1 is:
(let* ((yin C_0)
(yang
(g ###)))
(yin yang))
### is placeholder. Note that in this continuation, yin's value is determined (that's what let* do). We are sure that yin's value is C_0 here.
Since (id C_1) is C_1, so yang's value is
(g C_1)
g has a side effect -- outputting *. So the program does.
yang's value is now C_1.
By now, we have displayed @*
So now it becomes:
(let* ((yin C_0)
(yang C_1))
(yin yang))
As both yin and yang are solved, we should evaluate (yin yang). It's
(C_0 C_1)
Holy SH*T!
But finally, C_0 is called. So we fly into the C_0 universe and forget all about these sh*ts. We will never go back to this universe again.
Round 1
C_0 take with C_1 back. The program now becomes(If you forget what C_0 stands for, go back to see it):
(let* ((yin
(f C_1))
(yang
(g (call-with-current-continuation id))))
(yin yang))
Ah, we find that yin's value is not determined yet. So we evaluate it. In the process of evaluating yin, we output an @ as f's side effect. And we know yin is C_1 now.
We begin to evaluate yang, we came across call-with-current-continuation again. We are practiced. We create a continuation C_2 which stands for:
(let* ((yin C_1)
(yang
(g ###)))
(yin yang))
And we display a * as g executing. And we come here
(let* ((yin C_1)
(yang C_2))
(yin yang))
So we got:
(C_1 C_2)
You know where we are going. We are going to C_1's universe. We recall it from memory(or copy and paste from webpage). It is now:
(let* ((yin C_0)
(yang
(g C_2)))
(yin yang))
We know in C_1's universe, yin's value has been determined. So we begin to evaluate yang. As we are practiced, I will directly tell you that it displays * and becomes:
(C_0 C_2)
Now we have printed @*@**, and we are going to C_0's universe taking with C_2.
Round 2
As we are practiced, I will tell you that we display '@', yin is C_2, and we create a new continuation C_3, which stands for:
(let* ((yin C_2)
(yang
(g ###)))
(yin yang))
And we display *, yang is C_3, and it becomes
(C_2 C_3)
And we can continue. But I will stop here, I have showed you what Yin-Yang puzzle's first several outputs are.
Why the number of * increases?
Now your head is full of details. I will make a summary for you.
I will use a Haskell like syntax to simplify. And cc is short for call-with-current-continuation.
When #C_i# is bracketed by #, it means the continuation is create here. ; means output
yin = f cc id
yang = g cc id
yin yang
---
yin = f #C_0# ; @
yang = g cc id
yin yang
---
yin = C_0
yang = g #C_1# ; *
yin yang
---
C_0 C_1
---
yin = f C_1 ; @
yang = g #C_2# ; *
yin yang
---
C_1 C_2
---
yin = C_0
yang = g C_2 ; *
yin yang
---
C_0 C_2
---
yin = f C_2 ; @
yang = g #C_3#; *
yin yang
---
C_2 C_3
---
yin = C_1
yang = g C_3 ; *
yin yang
---
C_1 C_3
---
yin = C_0
yang = g C_3 ; *
yin yang
---
C_0 C_3
If you observe carefully, it will be obvious to you that
- There are lots of universes(in fact infinite), but
C_0 is the only universe that started by f. Others is started by g.
C_0 C_n always makes a new continuation C_max. It's because C_0 is the first universe which g cc id has not been executed.C_0 C_n also display @. C_n C_m which n is not 0 will display *.- Time by time the program is deduced to
C_0 C_n, and I will prove that C_0 C_n is separated by more and more other expression, which leads to @*@**@***...
A little bit math
Assume 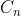 (n != 0) is the biggest numbered in all continuations, and then
(n != 0) is the biggest numbered in all continuations, and then C_0 C_n is called.
Assumption: When C_0 C_n is called, C_n is the current maximum numbered continuation.
Now 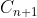 is created by
is created by C_0 C_n like this:
yin = f C_n ; @
yang = g #C_{n+1}#
yin yang
So we conclude that:
Theorem I. If C_0 C_n is called, It will produce a continuation 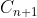 , in which
, in which yin is C_n.
Then next step is C_n C_{n+1}.
yin = C_{n-1}
yang = g C_{n+1} ; *
yin yang
The reason why yin is C_{n-1} is that When C_n being created it obeyed Theorem I.
And then C_{n-1} C_{n+1} is called, and we know when C_{n-1} is created, it also obeyed Theorem I. So We have C_{n-2} C_{n+1}.
C_{n+1} is the in-variation. So we have the second theorem:
Theorem II. If C_n C_m which n < m and n > 0 is called, It will become C_{n-1} C_m.
And we have Manually checked C_0 C_1 C_2 C_3. They obey the Assumption and all Theorems. And we know how first @ and * is created.
So we can write patterns below.
C_0 C_1 ; @ *
C_[1-0] C_2 ; @ * *
C_[2-0] C_3 ; @ * * *
...
It not so strict, but I'd like to write:
Q.E.D.
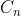 (n != 0) is the biggest numbered in all continuations, and then
(n != 0) is the biggest numbered in all continuations, and then 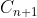 is created by
is created by