Construct 4 arrays:
1: Every element is the element from original array + one to the left.
2: Every element is the element from original array + one to the top.
3: Every element is the element from original array + one to the top left.
4: Every element is the element from original array + one to the top right.
You would get something like this for your array.
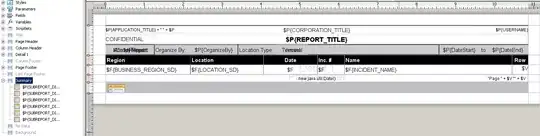 Now you have to check every possible square fitting in the array (There possibly is better solution, but I can't think of any) looking for something like this in other four.
Now you have to check every possible square fitting in the array (There possibly is better solution, but I can't think of any) looking for something like this in other four.
 Since we keep sums in the array we can clearly see that when checking an array 3x3 (from top left) all sums are 15. It means it's a magic square.
Since we keep sums in the array we can clearly see that when checking an array 3x3 (from top left) all sums are 15. It means it's a magic square.
When not starting in top left it's a little less obvious but still easy. Look at example below with second magic square highlighted.
 You can see that evey darker element minus corresponding lighter element is constant (in this case 12)
You can see that evey darker element minus corresponding lighter element is constant (in this case 12)
It would work same for the first magic square, but there would be zeroes, so we can skip it.
 Now you have to check every possible square fitting in the array (There possibly is better solution, but I can't think of any) looking for something like this in other four.
Now you have to check every possible square fitting in the array (There possibly is better solution, but I can't think of any) looking for something like this in other four.
 Since we keep sums in the array we can clearly see that when checking an array 3x3 (from top left) all sums are 15. It means it's a magic square.
Since we keep sums in the array we can clearly see that when checking an array 3x3 (from top left) all sums are 15. It means it's a magic square. You can see that evey darker element minus corresponding lighter element is constant (in this case 12)
You can see that evey darker element minus corresponding lighter element is constant (in this case 12)