4

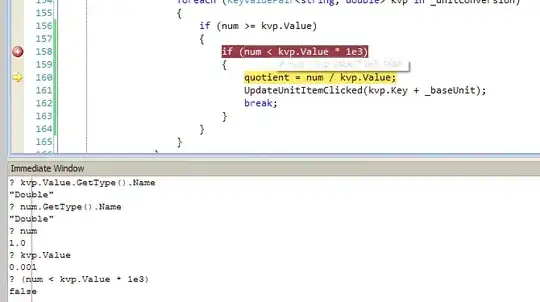
Consider we have a network flow and using Edmond-Karp algorithm, we already have the maximum flow on the network. Now, if we add an arbitrary edge (with certain capacity) to the network, what is the best way to update the maximum flow? I was thinking about updating the residual network regarding the new edge and again look for augmenting path until we find new max flow, but I am not sure if it works or if it is the best way!

Nima
  • 276
  • 3
  • 15

2 Answers2

4

After doing maxflow you know the amount of content each edge flowed.

So, when the cost of an edge changed you can do the following things :

  1. Suppose, the content flowed by that edge is w.
  2. Now do a forward dfs and a backward dfs from that edge and undone total w content from the edge it linked.

enter image description here

Here each edge is represented by x/y, where y means the edge capacity and x means the content it flowed.

Now you want to change the cost of edge 4->3 from 2 to 3.

All you have to do is do a forward and backward dfs from 4->3 edge and undone 2 weight from these edge as 4->3 flowed w=2 content.

Here is the process will look like :

enter image description here

Now you are almost done :)

  1. Change the cost of the edge 4->3 from 2 to 3 and again try to find an augmenting path :)

Let me know if you find it difficult to understand or if i'm wrong somehow :)

Edit :

  1. If new edge cost is greater than current cost than you won't have to undone the weight. You can just try to find an augmenting path changing the edge's capacity.

  2. But if the capacity reduced, you have to undone the weight and try to find an augmenting path.

  3. If a new edge added, you can just add the edge and try to find an augmenting path if available. that's it.

Ali Akber
  • 3,670
  • 3
  • 26
  • 40
  • Thanks a lot. I have two further questions. First, Why do we need to undone the weight 2 anyway? Why cannot we just change the capacity, and check for augmenting path? I am thinking that if it is one of the edges in a min-cut then we may be able to send more flow through it otherwise it is not possible to send more flow because the min-cut constraints the flow! Second, your answer mentions a change in capacity. What if I add one new edge? For example add the edge ***4->6*** with capacity 4? – Nima Dec 13 '14 at 20:02
  • Nice question. okay think about the case where new edge cost is greater than current cost that is in our example edge 4->3 changes to 3 from 2. In this case you won't have to undone the weight. You can just try to find an augmenting path changing the edge's capacity to 3. But what if the capacity reduced? that is 4->3 capacity reduces to 0. then i think previous technique won't work so you have to undone the weight and try to find an augmenting path. And for the 2nd question, you can just add the edge and try to find an augmenting path if available. that's it. because here you get a new path. – Ali Akber Dec 14 '14 at 05:31
  • Ok, I got it. Just one more question! When there are multiple path from source to beginning of the edge changed or multiple path from end node of changed edge to the sink. How do we decide to undo the flow of which path?!!! For instance, Here are multiple path from 3 to 7. Hence there are different ways to undo the flow. How, should I choose which path(s) to choose for undoing? – Nima Dec 14 '14 at 21:23
  • You can choose any path. The main task is to undo the weight. And as you know water can flow where it can find a tiny hole :) so there won't be a problem regarding maxflow :) you just need to make the hole ... – Ali Akber Dec 15 '14 at 07:26
0

Actually adding a new edge is not very difficult - you have the flows/ capacities of the edges before adding the edge and then you add the edge and its inverse. Then run the algorithm you use to find augmenting path until you find non-zero flow and that's it. Most of the max flow will already have been found so this should(in theory) not be too slow. I do not know which max flow algorithm you are using so I can not be more specific, but it is possible that after adding the new edge you violate the property of the algorithm and thus you find the max flow in a sub-optimal way. Still you've already processed most of the graph so this should not be a too big problem.

I would recommend you to use Ford-Fulkerson algorithm to finish of the task no matter what the original algorithm you used for the max flow is. I think it will perform well in cases that most of the max flow is already discovered.

Ivaylo Strandjev
  • 69,226
  • 18
  • 123
  • 176
  • Actually, I am using Edmond-Karp algorithm, which is a variation of Ford-Fulkerson. The only difference is that in each step for finding the augmenting path, it uses BFS, so it will have minimum number of edges. it makes it possible to prove that with integer capacities we can do the job in polynomial time! – Nima Dec 13 '14 at 19:54
  • Ok. That should do it even better. – Ivaylo Strandjev Dec 13 '14 at 19:56