Code to resemble a rowing stroke

Question

I'm working on a small program displaying moving rowing boats. The following shows a simple sample code (Python 2.x):

import time
class Boat:
    def __init__(self, pace, spm):
        self.pace = pace  #velocity of the boat in m/s
        self.spm = spm    #strokes per minute
        self.distance = 0 #distance travelled

    def move(self, deltaT):
        self.distance = self.distance + (self.pace * deltaT)

boat1 = Boat(3.33, 20)
while True:
    boat1.move(0.1)
    print boat1.distance
    time.sleep(0.1)

As you can see a boat has a pace and rows with a number of strokes per minute. Everytime the method move(deltaT) is called it moves a certain distance according to the pace.

The above boat just travels at a constant pace which is not realistic. A real rowing boat accelerates at the beginning of a stroke and then decelerates after the rowing blades left the water. There are many graphs online which show a typical rowing curve (force shown here, velocity looks similar):

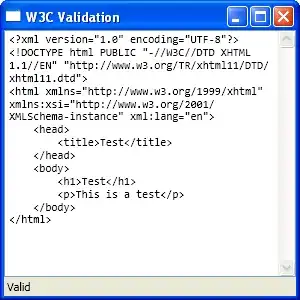Source: highperformancerowing.net

The pace should be constant over time, but it should change during the stroke.

What is the best way to change the constant velocity into a curve which (at least basically) resembles a more realistic rowing stroke?

Note: Any ideas on how to tag this question better? Is it an algorithm-problem?

Answer 1

If your goal is to simply come up with something visually plausible and not to do a full physical simulation, you can simply add a sine wave to the position.

class Boat:
    def __init__(self, pace, spm, var=0.5):
        self.pace = pace    #average velocity of the boat in m/s
        self.sps = spm/60.0 #strokes per second
        self.var = var      #variation in speed from 0-1
        self.totalT = 0     #total time
        self.distance = 0   #distance traveled

    def move(self, deltaT):
        self.totalT += deltaT
        self.distance = self.pace * (self.totalT + self.var * math.sin(self.totalT * self.sps * 2*math.pi)

You need to be careful with the variation var, if it gets too high the boat might go backwards and destroy the illusion.

Answer 2

You can convert a curve like this into a polynomial equation for velocity.

A description/example of how to do this can be found at:

python numpy/scipy curve fitting

This shows you how to take a set of x,y coordinates (which you can get by inspection of your existing plot or from actual data) and create a polynomial function.

If you are using the same curve for each Boat object, you could just hard code it into your program. But you could also have a separate polynomial equation for each Boat object as well, assuming each rower or boat has a different profile.

Answer 3

You can perform simple integration of the differential equation of motion. (This is what you are already doing to get space as a function of time, with constant speed, x' = x + V.dt.)

Assume a simple model with a constant force during the stroke and no force during the glide, and drag proportional to the speed.

So the acceleration is a = P - D.v during stroke, and - D.v during glide (deceleration).

The speed is approximated with v' = v + a.dt.

The space is approximated with x' = x + v.dt.

If dt is sufficiently small, this motion should look realistic. You can refine the model with a more accurate force law and better integration techniques like Runge-Kutta, but I am not sure it is worth it.

Below an example plot of speed and space vs time using this technique. It shows speed oscillations quickly establishing a periodic regime, and quasi-linear displacement with undulations.