Points closest to an estimated path

Question

Similar to my previous question: Closest point to a path

I would like to be able to find all the centers that are closest to a path. However some of the data is missing from the path, and I would like to do linear segments to interpolate between points to 'estimate' a possible path, and still find likely centers that would have been close to that 'estimated path'.

set.seed(1)
n <- 10000
x <- 100*cumprod(1 + rnorm(n, 0.0001, 0.002))
y <- 50*cumprod(1 + rnorm(n, 0.0001, 0.002))

# original path
path <- data.frame(cbind(x=x, y=y))

# path with missing points/points every hundred
path.w.missing <- path[seq(1,n,by=100),]


centers <- expand.grid(x=seq(0, 500,by=0.5) + rnorm(1001), 
                       y=seq(0, 500, by=0.2) + rnorm(2501))

centers$id <- seq(nrow(centers))

Short of simulating millions of linear points between the given points in the path....I'm not sure how one would go about doing this...

To me its a bit like finding the intersection of a line and a matrix of cells...of sorts....but perhaps I'm miles off...

Any help would be greatly appreciated.

Answer 1

Would this help:

## create data
set.seed(1)
n <- 10000
x <- 100 * cumprod(1 + rnorm(n, 0.0001, 0.002))
y <- 50 * cumprod(1 + rnorm(n, 0.0001, 0.002))

# original path
path <- data.frame(cbind(x=x, y=y))

# path with missing points/points every hundred
path.w.missing <- path[seq(1,n,by=100),]


## proposed solution
library(raster)

l <- SpatialLines(list(Lines(list(Line(path.w.missing)), "1")))
r <- raster(extent(bbox(l)), res = c(0.5, 0.2))
r <- rasterize(l, r, field = 1)

## xy will be a matrix
xy <- rasterToPoints(r)

plot(r)
points(xy)
points(path.w.missing, col = "red")

Answer 2

The package marmap does exactly what you need:

library(marmap)
bcenters <- as.bathy(centers)
out <- path.profile(path.w.missing,bcenters)

       lon      lat   dist.km  depth
2 100.0512 50.04129   0.00000 247451
3 101.2070 50.11430  82.87177 247450
4 101.3687 50.18730  95.33454 247449
5 101.5973 50.26030 112.81665 248453
6 102.6877 50.33330 190.48139 248454
7 103.2105 50.40630 228.37510 248458

The id is in the column depth. This function was coded to retrieve depth in a bathymetric matrix along a path. It finds all cells of the bathymetric matrix "bellow" the path (i.e. cells closest to the path) and outputs the value of these cells. By transforming your centers object into a matrix of class bathy, your column id is used as if it was the depth. Thus path.profile() outputs the id of the cells closest to your path in the depth column.

Here, you start with 100 points in your path.w.missing object. path.profile() gets you the id of the

nrow(out)
795

cells that are closest to this path.

Here is a plot of the path.w.missing data with the closest points overlaid in red:

plot(path.w.missing,type="o",cex=.3, lwd=5)
points(out[,1],out[,2], col=rgb(1,0,0,.8), cex=.3)

Answer 3

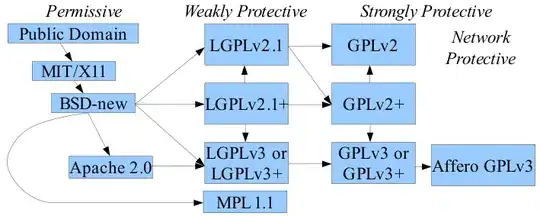
Use the smooth.spline function (Fit a Smoothing Spline)

mx=path.w.missing$x
my=path.w.missing$y
s<-smooth.spline(mx,my)
plot(mx,my)
lines(s) #draw the estimated path 

predict(s,1:10) #And now you can generate all the points on the estimated path

> predict(s,1:10)
$x
 [1]  1  2  3  4  5  6  7  8  9 10

$y
 [1] 2.418294 2.904019 3.389744 3.875469 4.361195 4.846920 5.332645 5.818370 6.304095 6.789820

And you can use the Linear model to fit it.

> summary(lm(my~mx))

Call:
lm(formula = my ~ mx)

Residuals:
    Min      1Q  Median      3Q     Max 
-12.772  -8.642   3.112   5.831  17.237 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -12.60098    3.46583  -3.636 0.000444 ***
mx            0.56579    0.02138  26.469  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 7.896 on 98 degrees of freedom
Multiple R-squared:  0.8773,    Adjusted R-squared:  0.876 
F-statistic: 700.6 on 1 and 98 DF,  p-value: < 2.2e-16

as you can see,p<0.05,so my and mx can fit as a line:

my=-12.60098+0.56579*mx

ggplot2 can draw this line easily:

 d=data.frame(mx,my)
 library(ggplot2)
 ggplot(d,aes(mx,my))+geom_point()+geom_smooth(method="lm")

assume that a line is Ax+By+C=0 and the point is(X0，Y0),point to the line distance：

|AX0+BY0+C|/√(A²+B²)

so in this case, 0.56579*mx-my-12.60098=0 ,A=0.56579,B=-1,C=-12.60098 ,it's easy to calculate the distance from point to line and find the closest point to the line.

Further more,if you want to find the closest point , remove the denominator √(A²+B²) would not affect the sort,so,the optimization of the formula:

|AX0+BY0+C|

Result

> for(i in 1:2503501){
+ temp=abs(centers[[1]][i]*0.56579-centers[[2]][i]-12.60098)
+ if(m>temp){
+ m=temp
+ pos=i
+ }
+ }
> m
[1] 2.523392e-05
> pos
[1] 638133

Use the Rcpp to accelerate the program "test.cpp"

#include <Rcpp.h>
using namespace Rcpp;

// [[Rcpp::export]]
int closest(NumericVector a, NumericVector b) {
  int length = a.size();
  double temp,m=10000;
  int pos=0;
  for(int i=0;i<length;i++){
    temp=a[i]*0.56579-b[i]-12.60098;
    if(temp>=0){
      if(m>temp){m=temp;pos=i;}      
    }else{
      if(m>-temp){m=-temp;pos=i;}
    }
  }
  return pos+1;
}

Result(the Rcpp cost about 2 seconds):

> sourceCpp("test.cpp")
> closest(centers[[1]],centers[[2]])
[1] 974698
> abs(centers[[1]][974698]*0.56579-centers[[2]][974698]-12.60098)
[1] 0.0002597022