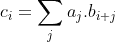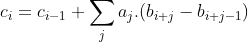Efficient bitstream convolution

Question

I have two floating point time series A, B of length N each. I have to calculate the circular convolution and find maximum value. The classic and fastest way of doing this is

C = iFFT(FFT(A) * FFT(B))

Now, let's suppose that both A and B is a series which contains only 1s and 0s, so in principle we can represent them as bitstreams.

Question: Is there any faster way of doing the convolution (and find its maximum value) if I am somehow able to make use of the fact above ?

(I was already thinking a lot on Walsh - Hadamard transforms and SSE instructions, popcounts, but found no faster way for M > 2 **20 which is my case.)

Thanks, gd

Answer 1

The 1D convolution c of two arrays a and b of size n is an array such that :

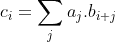
This formula can be rewritten in an iterative way :

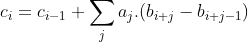
The non-null terms of the sum are limited to the number of changes nb of b : if b is a simple pattern, this sum can be limited to a few terms. An algorithm may now be designed to compute c :

1 : compute c[0] (about n operations)

2 : for 0<i<n compute c[i] using the formula (about nb*n operations)

If nb is small, this method may be faster than fft. Note that it will provide exact results for bitstream signals, while the fft needs oversampling and floating point precision to deliver accurate results.

Here is a piece of code implementing this trick with input type unsigned char.

#include <stdlib.h>
#include <math.h>
#include <string.h>
#include <time.h>

#include <fftw3.h>

typedef struct{
    unsigned int nbchange;
    unsigned int index[1000];
    int change[1000];
}pattern;

void topattern(unsigned int n, unsigned char* b,pattern* bp){
    //initialisation
    bp->nbchange=0;
    unsigned int i;
    unsigned char former=b[n-1];
    for(i=0;i<n;i++){
        if(b[i]!=former){
            bp->index[bp->nbchange]=i;
            bp->change[bp->nbchange]=((int)b[i])-former;
            bp->nbchange++;
        }
        former=b[i];
    }
}

void printpattern(pattern* bp){
    int i;
    printf("pattern :\n");
    for(i=0;i<bp->nbchange;i++){
        printf("index %d change %d\n",bp->index[i],bp->change[i]);
    } 
}

//https://stackoverflow.com/questions/109023/how-to-count-the-number-of-set-bits-in-a-32-bit-integer

unsigned int NumberOfSetBits(unsigned int i)
{
    i = i - ((i >> 1) & 0x55555555);
    i = (i & 0x33333333) + ((i >> 2) & 0x33333333);
    return (((i + (i >> 4)) & 0x0F0F0F0F) * 0x01010101) >> 24;
}

//https://stackoverflow.com/questions/2525310/how-to-define-and-work-with-an-array-of-bits-in-c

unsigned int convol_longint(unsigned int a, unsigned int b){
    return NumberOfSetBits(a&b);
}

int main(int argc, char* argv[]) {

    unsigned int n=10000000;

    //the array a
    unsigned char* a=malloc(n*sizeof(unsigned char));
    if(a==NULL){printf("malloc failed\n");exit(1);}
    unsigned int i,j;
    for(i=0;i<n;i++){
        a[i]=rand();
    }
    memset(&a[2],5,2);
    memset(&a[10002],255,20);

    for(i=0;i<n;i++){
        //printf("a %d %d \n",i,a[i]);
    }

    //pattern b
    unsigned char* b=malloc(n*sizeof(unsigned char));
    if(b==NULL){printf("malloc failed\n");exit(1);}
    memset(b,0,n*sizeof(unsigned char));
    memset(&b[2],1,20);


    //memset(&b[120],1,10);
    //memset(&b[200],1,10);

    int* c=malloc(n*sizeof(int)); //nb bit in the array
    memset(c,0,n*sizeof(int));

    clock_t begin, end;
    double time_spent;

    begin = clock();
    /* here, do your time-consuming job */


    //computing c[0]
    for(i=0;i<n;i++){
        //c[0]+= convol_longint(a[i],b[i]);
        c[0]+= ((int)a[i])*((int)b[i]);
        //printf("c[0] %d %d\n",c[0],i);
    }
    printf("c[0] %d\n",c[0]);

    //need to store b as a pattern.
    pattern bpat;
    topattern( n,b,&bpat);
    printpattern(&bpat);

    //computing c[i] according to formula
    for(i=1;i<n;i++){
        c[i]=c[i-1];
        for(j=0;j<bpat.nbchange;j++){
            c[i]+=bpat.change[j]*((int)a[(bpat.index[j]-i+n)%n]);
        }
    }

    //finding max
    int currmax=c[0];
    unsigned int currindex=0;
    for(i=1;i<n;i++){
        if(c[i]>currmax){
            currmax=c[i];
            currindex=i;
        }
        //printf("c[i] %d %d\n",i,c[i]);
    }

    printf("c[max] is %d at index %d\n",currmax,currindex);

    end = clock();
    time_spent = (double)(end - begin) / CLOCKS_PER_SEC;

    printf("computation took %lf seconds\n",time_spent);


    double* dp = malloc(sizeof (double) * n);
    fftw_complex * cp = fftw_malloc(sizeof (fftw_complex) * (n/2+1));

    begin = clock();
    fftw_plan plan = fftw_plan_dft_r2c_1d(n, dp, cp, FFTW_ESTIMATE);

    end = clock();
    time_spent = (double)(end - begin) / CLOCKS_PER_SEC;

    fftw_execute ( plan );
    printf("fftw took %lf seconds\n",time_spent);

    free(dp);
    free(cp);

    free(a);
    free(b);
    free(c);
    return 0;
}

To compile : gcc main.c -o main -lfftw3 -lm

For n=10 000 000 and nb=2 (b is just a "rectangular 1D window") this algorithm run in 0.65 seconds on my computer. A double-precision fft using fftw took approximately the same time. This comparison, like most of comparisons, may be unfair since :

• nb=2 is the best case for the algorithm presented in this answer.
• The fft-based algorithm would have needed oversampling.
• double precison may not be required for the fft-based algorithm
• The implementation exposed here is not optimized. It is just basic code.

This implementation can handle n=100 000 000. At this point, using long int for c could be advised to avoid any risk of overflow.

If signals are bitstreams, this program may be optimzed in various ways. For bitwise operations, look this question and this one