Performance comparison Fortran, Numpy,Cython and Numexpr

Question

I have following function:

def get_denom(n_comp,qs,x,cp,cs):
'''
len(n_comp) = 1 # number of proteins
len(cp) = n_comp # protein concentration
len(qp) = n_comp # protein capacity
len(x) = 3*n_comp + 1 # fit parameters
len(cs) = 1

'''
    k = x[0:n_comp]
    sigma = x[n_comp:2*n_comp]
    z = x[2*n_comp:3*n_comp]

    a = (sigma + z)*( k*(qs/cs)**(z-1) )*cp
    denom = np.sum(a) + cs
    return denom

I compare it against a Fortran implementation (My first Fortran function ever):

subroutine get_denom (qs,x,cp,cs,n_comp,denom)

! Calculates the denominator in the SMA model (Brooks and Cramer 1992)
! The function is called at a specific salt concentration and isotherm point
! I loops over the number of components

implicit none

! declaration of input variables
integer, intent(in) :: n_comp ! number of components
double precision, intent(in) :: cs,qs ! salt concentration, free ligand concentration
double precision, dimension(n_comp), INTENT(IN) ::cp ! protein concentration
double precision, dimension(3*n_comp + 1), INTENT(IN) :: x ! parameters

! declaration of local variables
double precision, dimension(n_comp) :: k,sigma,z
double precision :: a
integer :: i

! declaration of outpur variables
double precision, intent(out) :: denom

k = x(1:n_comp) ! equlibrium constant
sigma = x(n_comp+1:2*n_comp) ! steric hindrance factor
z = x(2*n_comp+1:3*n_comp) ! charge of protein

a = 0.
do i = 1,n_comp
    a = a + (sigma(i) + z(i))*(k(i)*(qs/cs)**(z(i)-1.))*cp(i)
end do

denom = a + cs

end subroutine get_denom

I compiled the .f95 file by using:

1) f2py -c -m get_denom get_denom.f95 --fcompiler=gfortran

2) f2py -c -m get_denom_vec get_denom.f95 --fcompiler=gfortran --f90flags='-msse2' (The last option should turn on auto-vectorization)

I test the functions by:

import numpy as np
import get_denom as fort_denom
import get_denom_vec as fort_denom_vec
from matplotlib import pyplot as plt
%matplotlib inline

def get_denom(n_comp,qs,x,cp,cs):
    k = x[0:n_comp]
    sigma = x[n_comp:2*n_comp]
    z = x[2*n_comp:3*n_comp]
    # calculates the denominator in Equ 14a - 14c (Brooks & Cramer 1992)
    a = (sigma + z)*( k*(qs/cs)**(z-1) )*cp
    denom = np.sum(a) + cs
    return denom

n_comp = 100
cp = np.tile(1.243,n_comp)
cs = 100.
qs = np.tile(1100.,n_comp)
x= np.random.rand(3*n_comp+1)
denom = np.empty(1)
%timeit get_denom(n_comp,qs,x,cp,cs)
%timeit fort_denom.get_denom(qs,x,cp,cs,n_comp)
%timeit fort_denom_vec.get_denom(qs,x,cp,cs,n_comp)

I added following Cython code:

import cython
# import both numpy and the Cython declarations for numpy
import numpy as np
cimport numpy as np

@cython.boundscheck(False)
@cython.wraparound(False)
def get_denom(int n_comp,np.ndarray[double, ndim=1, mode='c'] qs, np.ndarray[double, ndim=1, mode='c'] x,np.ndarray[double, ndim=1, mode='c'] cp, double cs):

    cdef int i
    cdef double a
    cdef double denom   
    cdef double[:] k = x[0:n_comp]
    cdef double[:] sigma = x[n_comp:2*n_comp]
    cdef double[:] z = x[2*n_comp:3*n_comp]
    # calculates the denominator in Equ 14a - 14c (Brooks & Cramer 1992)
    a = 0.
    for i in range(n_comp):
    #a += (sigma[i] + z[i])*( pow( k[i]*(qs[i]/cs), (z[i]-1) ) )*cp[i]
        a += (sigma[i] + z[i])*( k[i]*(qs[i]/cs)**(z[i]-1) )*cp[i]

    denom = a + cs

    return denom

EDIT:

Added Numexpr, using one thread:

def get_denom_numexp(n_comp,qs,x,cp,cs):
    k = x[0:n_comp]
    sigma = x[n_comp:2*n_comp]
    z = x[2*n_comp:3*n_comp]
    # calculates the denominator in Equ 14a - 14c (Brooks & Cramer 1992)
    a = ne.evaluate('(sigma + z)*( k*(qs/cs)**(z-1) )*cp' )
    return cs + np.sum(a)

ne.set_num_threads(1)  # using just 1 thread
%timeit get_denom_numexp(n_comp,qs,x,cp,cs)

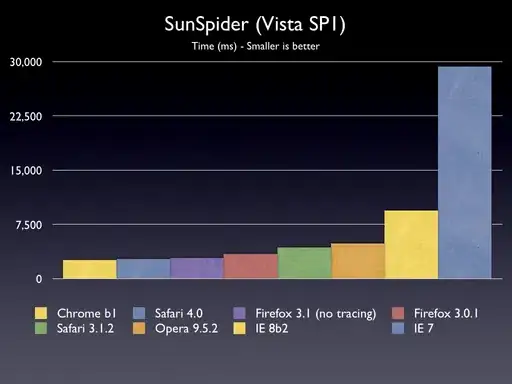
The result is (smaller is better):

Why is is the speed of Fortran getting closer to Numpy with increasing size of the arrays? And how could i speed up Cython? Using pointers?

Answer 1

Sussed It.

OK, finally, we were permitted to install Numpy etc on one of our boxes, and that has allowed what may be a comprehensive explanation of your original post.

The short answer is that your original questions is, in a sense, "the wrong question". In addition, there has been much vexatious abuse and misinformation by one of the contributors, and those errors and fabrications deserve attention, lest anyone make the mistake of believing them, and to their cost.

Also, I have decided to submit this answer as a separate answer, rather than editing my answer of Apr 14, for reasons seen below, and propriety.

Part A: The Answer to the OP

First things first, dealing with the question in the original post: You may recall I could only comment wrt to the Fortran side, since our policies are strict about what software may be installed and where on our machines, and we did not have Python etc to hand (until just now). I had also repeatedly stated that the character of your result was interesting in terms of what we can call its curved character or perhaps "concavity".

In addition, working purely with "relative" results (as you did not post the absolute timings, and I did not have Numpy to hand at the time), I had indicated a few times that some important information may be lurking therein.

That is precisely the case.

First, I wanted to be sure I could reproduce your results, since we don't use Python/F2py normally, it was not obvious what compiler settings etc are implied in your results, so I performed a variety of tests to be sure we are talking apples-to-apples (my Apr 14 answer demonstrated that Debug vs Release/O2 makes a big difference).

Figure 1 shows my Python results for just the three cases of: your original Python/Numpy internal sub-program (call this P, I just cut/pasted your original), your original Do based Fortran s/r you had posted (call this FDo, I just copy/pasted your original, as before), and one of the variations I had suggested earlier relying on Array Sections, and thus requiring Sum() (call this FSAS, created by editing your original FDo). Figure 1 shows the absolute timings via timeit.

Figure 2 shows the relative results based on your relative strategy of dividing by the Python/Numpy (P) timings. Only the two (relative) Fortran variants are shown.

Clearly, those reproduce the character in your original plot, and we may be confident that my tests seem to be consistent with your tests.

Now, your original question was "Why is is the speed of Fortran getting closer to Numpy with increasing size of the arrays?".

In fact, it is not. It is purely an artefact/distortion of relying purely on "relative" timings that may give that impression.

Looking at Figure 1, with the absolute timings, it is clear the Numpy and Fortran are diverging. So, in fact, the Fortran results are moving away from Numpy or vice versa, if you like.

A better question, and one which arose repeatedly in my previous comments, is why are these upward curving in the first place (c.f. linear, for example)? My previous Fortran-only results showed a "mostly" flat relative performance ratio (yellow lines in my Apr 14 chart/answer), and so I had speculated that there was something interesting happening on the Python side and suggested checking that.

One way to show this is with yet a different kind of relative measure. I divided each (absolute) series with its own highest value (i.e. at n_comp = 10k), to see how this "internal relative" performance unfolds (those are referred to as the ??10k values, representing the timings for n_comp = 10,000). Figure 3 shows these results for P, FDo, and FSAS as P/P10k, FDo/FDo10k, and FSAS/FSAS10k. For clarity, the y-axis has a logarithmic scale. It is clear that the Fortran variants preform relatively very much better with decreasing n_comp c.f. the P results (e.g. the red circle annotated section).

Put differently, Fortran is very very (non-linearly) more efficient for decreasing array size. Not sure exactly why Python would do so much worse with decreasing n_comp ... but there it is, and may be an issue with internal overhead/set-up etc., and the differences between interpreters vs compilers etc.

So, it's not that Fortran is "catching up" with Python, quite the opposite, it is continuing to distance itself from Python (see Figure 1). However, the differences in the non-linearities between Python and Fortran with decreasing n_comp produce "relative" timings with apparently counter-intuitive and non-linear character.

Thus, as n_comp increases and each method "stabilises" to a more or less linear mode, the curves flatten to show that their differences are growing linearly, and the relative ratios settle to an approximate constant (ignoring memory contention, smp issues, etc.) ... this is easier to see if n_comp is allowed > 10k, but the yellow line in my Apr 14 answer already show this for the Fortran-only s/r's.

Aside: My preference is to create my own timing routines/functions. timeit seems convenient, but there is much going on inside that "black box". Setting your own loops and structures, and being certain of the properties/resolution of your timing functions is important towards a proper assessment.

Answer 2

Being named in the other answer, I have to respond.

I know this does not really answer the original question, but the original poster encouraged pursuing this direction in his comments.

My points are these:

1. I do not believe the array intrinsic are better optimized in any way. If one is lucky, they are translated to the same loop code as the manual loops. If one is not, performance problems can arise. Therefore, one has to be careful. There is a potential to trigger temporary arrays.

I translated the offered SAS arrays to usual do loop. I call it DOS. I demonstrate the DO loops are in no way slower, both subroutines result in more or less the same code in this case.

qsDcs = qs/cs

denom = 0
do j = 1, n_comp
  denom = denom + (x(n_comp+j) + x(2*n_comp+j)) * (x(j)*(qsDcs)**(x(2*n_comp+j)-1))*cp(j)
end do

denom = denom + cs

It is important to say that I don't believe this version is less readable just because it has one or two more lines. It is actually quite straightforward too see what is happening here.

Now the timings for these

f2py -c -m sas  sas.f90 --opt='-Ofast'
f2py -c -m dos  dos.f90 --opt='-Ofast'


In [24]: %timeit test_sas(10000)
1000 loops, best of 3: 796 µs per loop

In [25]: %timeit test_sas(10000)
1000 loops, best of 3: 793 µs per loop

In [26]: %timeit test_dos(10000)
1000 loops, best of 3: 795 µs per loop

In [27]: %timeit test_dos(10000)
1000 loops, best of 3: 797 µs per loop

They are just the same. There is no hidden performance magic in the array intrinsics and array expression arithmetic. In this case they are just translated to loops under the hood.

If you inspect the generated GIMPLE code, both the SAS and DOS are translated to the same main block of optimized code, no magical version of SUM() is called here:

  <bb 8>:
  # val.8_59 = PHI <val.8_49(9), 0.0(7)>
  # ivtmp.18_123 = PHI <ivtmp.18_122(9), 0(7)>
  # ivtmp.25_121 = PHI <ivtmp.25_120(9), ivtmp.25_117(7)>
  # ivtmp.28_116 = PHI <ivtmp.28_115(9), ivtmp.28_112(7)>
  _111 = (void *) ivtmp.25_121;
  _32 = MEM[base: _111, index: _106, step: 8, offset: 0B];
  _36 = MEM[base: _111, index: _99, step: 8, offset: 0B];
  _37 = _36 + _32;
  _40 = MEM[base: _111, offset: 0B];
  _41 = _36 - 1.0e+0;
  _42 = __builtin_pow (qsdcs_18, _41);
  _97 = (void *) ivtmp.28_116;
  _47 = MEM[base: _97, offset: 0B];
  _43 = _40 * _47;
  _44 = _43 * _42;
  _48 = _44 * _37;
  val.8_49 = val.8_59 + _48;
  ivtmp.18_122 = ivtmp.18_123 + 1;
  ivtmp.25_120 = ivtmp.25_121 + _118;
  ivtmp.28_115 = ivtmp.28_116 + _113;
  if (ivtmp.18_122 == _96)
    goto <bb 10>;
  else
    goto <bb 9>;

  <bb 9>:
  goto <bb 8>;

  <bb 10>:
  # val.8_13 = PHI <val.8_49(8), 0.0(6)>
  _51 = val.8_13 + _17;
  *denom_52(D) = _51;

the code is functionally identical to the do loop version, just the name of the variables are different.

---

2. They assumed shape array arguments (:) have a potential to degrade performance. Whereas the argument received in the assumed size argument (*) or explicit size (n) is always simply contiguous, the assumed shape one theoretically does not have to be and the compiler must be prepared for that. Therefore I always recommend to use the contiguous attribute to your assumed shape arguments wherever you know you will call it with contiguous arrays.

In the other answer the change was quite pointless because it did not use any of the advantages of assumed shape arguments. Namely, that you do not have to pass the arguments with the array sizes and you can use the intrinsics such as size() and shape().

---

Here are the results of a comprehensive comparison. I made it to be as fair as possible. Fortran files are compiled with -Ofast as shown above:

import numpy as np
import dos as dos
import sas as sas
from matplotlib import pyplot as plt
import timeit
import numexpr as ne

#%matplotlib inline



ne.set_num_threads(1)

def test_n(n_comp):

    cp = np.tile(1.243,n_comp)
    cs = 100.
    qs = np.tile(1100.,n_comp)
    x= np.random.rand(3*n_comp+1)

    def test_dos():
        denom = np.empty(1)
        dos.get_denomsas(qs,x,cp,cs,n_comp)


    def test_sas():
        denom = np.empty(1)
        sas.get_denomsas(qs,x,cp,cs,n_comp)

    def get_denom():
        k = x[0:n_comp]
        sigma = x[n_comp:2*n_comp]
        z = x[2*n_comp:3*n_comp]
        # calculates the denominator in Equ 14a - 14c (Brooks & Cramer 1992)
        a = (sigma + z)*( k*(qs/cs)**(z-1) )*cp
        denom = np.sum(a) + cs
        return denom

    def get_denom_numexp():
        k = x[0:n_comp]
        sigma = x[n_comp:2*n_comp]
        z = x[2*n_comp:3*n_comp]
        loc_cp = cp
        loc_cs = cs
        loc_qs = qs
        # calculates the denominator in Equ 14a - 14c (Brooks & Cramer 1992)
        a = ne.evaluate('(sigma + z)*( k*(loc_qs/loc_cs)**(z-1) )*loc_cp' )
        return cs + np.sum(a)

    print 'py', timeit.Timer(get_denom).timeit(1000000/n_comp)
    print 'dos', timeit.Timer(test_dos).timeit(1000000/n_comp)
    print 'sas', timeit.Timer(test_sas).timeit(1000000/n_comp)
    print 'ne', timeit.Timer(get_denom_numexp).timeit(1000000/n_comp)


def test():
    for n in [10,100,1000,10000,100000,1000000]:
        print "-----"
        print n
        test_n(n)

Results:

            py              dos             sas             numexpr
10          11.2188110352   1.8704519272    1.8659651279    28.6881871223
100         1.6688809395    0.6675260067    0.667083025     3.4943861961
1000        0.7014708519    0.5406000614    0.5441288948    0.9069931507
10000       0.5825948715    0.5269498825    0.5309231281    0.6178650856
100000      0.5736029148    0.526198864     0.5304090977    0.5886831284
1000000     0.6355218887    0.5294830799    0.5366530418    0.5983200073
10000000    0.7903120518    0.5301260948    0.5367569923    0.6030929089

You can see that there is very small difference between the two Fortran versions. The array syntax is marginally slower, but nothing to speak about, really.

Conclusion 1: In this comparison overhead for all should be fair and you see that for ideal vector length Numpy and Numexpr CAN almost reach Fortran's performance, but when the vector is too small or perhaps even too large the overhead of the Python solutions prevails.

Conclusion 2: The higher performance SAS version in the other comparison is caused by comparing to the orginal OP's version which is not equivalent. The equivalent optimized DO loop version is included above in my answer.

Answer 3

Further to my previous answer, and Vladimir's weak speculation, I set up two s/r's: one as the original given, and one using array sections and Sum(). I also wished to demonstrate that Vladimir's remarks on Do loop optimisation as weak.

Also, a point I usually make for benchmarking, the size of n_comp in the example shown above is TOO small. The results below put each of the "original" and the "better" SumArraySection (SAS) variation into loops repeated 1,000 times inside the timing calls, so the results are for 1000 calcs of each s/r. If your timings are fractions of a second, they are likely unreliable.

There are a number of variations worth considering, none with explicit pointers. The one variation used for this illustrations is

subroutine get_denomSAS (qs,x,cp,cs,n_comp,denom)

! Calculates the denominator in the SMA model (Brooks and Cramer 1992)
! The function is called at a specific salt concentration and isotherm point
! I loops over the number of components

implicit none

! declaration of input variables
integer, intent(in) :: n_comp ! number of components
double precision, intent(in) :: cs,qs ! salt concentration, free ligand concentration
double precision, Intent(In)            :: cp(:)
double precision, Intent(In)            :: x(:)

! declaration of local variables
integer :: i

! declaration of outpur variables
double precision, intent(out) :: denom
!
!
double precision                        :: qsDcs
!
!
qsDcs = qs/cs
!
denom = Sum( (x(n_comp+1:2*n_comp) + x(2*n_comp+1:3*n_comp))*(x(1:n_comp)*(qsDcs) &
                                            **(x(2*n_comp+1:3*n_comp)-1))*cp(1:n_comp) ) + cs
!
!
end subroutine get_denomSAS

The key differences are:

a) passed arrays are (:) b) no array assignments in s/r, instead use array sections (equivalent to "effective " pointers). c) Use Sum() instead of Do

Then also try two different compiler optimisations to demonstrate implications.

As the two charts show, the orig code (blue diamonds) is much slower c.f. SAS (red squares) with low optimisation. SAS is still better with high optimisation, but they are getting close. This is in part explained by Sum() being "better optimised" when low compiler optimisation is used.

The yellow lines show the ratio between the two s/r's timings. Ignore the yellow line value at "0" in the top image (n_comp too small caused one of the timings to go wonky)

Since I don't have the user's original data to ratio against Numpy, I can make only the statement that the SAS curve on his chart should lie below his current Fortran results, and possibly be flatter or even down trending.

Put differently, there may not actually exist the divergence seen in the original posting, or at least not to that extent.

... though more experimentation may be helpful to demonstrate also the other comments/answers already provided.

Dear Moritz: oops, I forgot to mention, and pertaining to your question about pointers. As per earlier, a key reason for the improvement with the SAS variation is that it makes better use of "effective pointers" in that it obviates the need to reassign array x() into three new local arrays (i.e. since x is passed by ref, using array sections is a kind of pointer approach built into Fortran, and thus no need for explicit pointers), but then requires Sum() or Dot_Product() or whatever.

Instead, you can keep the Do and achieve something similar by changing x either to an n_compx3 2D array, or pass the three explicit 1D arrays of order n_comp directly. This decision would be, likely, driven by the size and complexity of your code, since it would require rewriting the calling/sr statements etc, and anywhere else x() is used. Some of our projects are > 300,000 lines of code, so in those case it is much much less expensive to change the code locally, such as to SAS etc.

I am still waiting to obtain permission to install Numpy on one of our boxes. As noted earlier, it is of some interest why your relative timings imply that Numpy improves with increasing n_comp ...

Of course, the comments about "proper" benchmarking etc, as well as the question of what compiler switches are implied by your use of fpy, still apply, as those may greatly alter the character of your results.

I would be interested to see your results if they were updated for these permutations.

Answer 4

There is not sufficient information in the notes, but some of the following may help:

1) Fortran has optimised intrinsic functions such as "Sum()" and "Dot_Product", which you may wish to use in place of the Do loop for summations etc.

In some cases (not neccessiraly here), it may be "better" to use a ForAll or whatever to create "meta" arrays to be summed, and then apply the summation on the "meta" arrays.

However, Fortran allows array sections so you don't need to create the automatic/intermediate arrays sigma, k, and z, and the releated overhead. Instead can have something like

n_compP1 = n_comp+1
n_compT2 = n_comp*2
a = Sum( x(1:n_comp)+2*x(n_compP1,n_compT2) )   ! ... just for example

2) Sometimes (depends on compiler, machine, etc), there can be "memory contentions" if the array sizes are not at certain "binary intervals" (e.g. 1024 vs. 1000) etc.

You may wish to repeat your experiments at a few more points in your chart (i.e. at various other "n_comps"), and particularly near such "boundaries".

3) Can't tell if you are using the full compiler optimsation (flags) for compiling your fortran code. You may wish to look up the various "-o" flags, etc.

4) You may wish to include OpemMP directive (or at least include openmp in your flags etc). That can sometimes improve certain overhead issues, even if not relying explicitly on OpenMP directives in your loops etc.

5) General: This would likely apply to each of your methods where loops are used

a) "constant operations" in the "summation" formula can be performed outside of the loop, eg. create something like qsDcs = qs/cs, and use qsDcs in the loop.

b) Similarly, sometimes it is useful to create something like zM1(:) = z(:) - 1, and use zM1(:) in the loop instead.