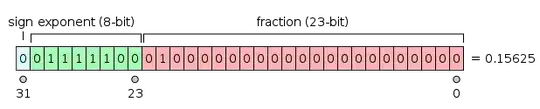
I write the following code in java and check the values stored in the variables. when I store 1.2 in a double variable 'y' it becomes 1.200000025443 something. Why it is not 1.200000000000 ?
public class DataTypes
{
static public void main(String[] args)
{
float a=1;
float b=1.2f;
float c=12e-1f;
float x=1.2f;
double y=x;
System.out.println("float a=1 shows a= "+a+"\nfloat b=1.2f shows b= "+b+"\nfloat c=12e-1f shows c= "+c+"\nfloat x=1.2f shows x= "+x+"\ndouble y=x shows y= "+y);
}
}
You can see the output here:
float a=1 shows a= 1.0 float b=1.2f shows b= 1.2 float c=12e-1f shows c= 1.2 float x=1.2f shows x= 1.2 double y=x shows y= 1.2000000476837158