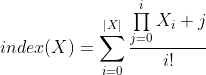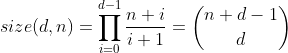1

This is the 3D version of an existing question.

A 3D array M[x,y,z] of shape (n,n,n) should be mapped to a flat vector containing only the elements with x<=y<=z in order to save space. So what I need is an expression similar to the 2D case (index := x + (y+1)*y/2). I tried to derive some formulas but just can't get it right. Note that the element order inside the vector doesn't matter.

Community
  • 1
  • 1
letmaik
  • 3,348
  • 1
  • 36
  • 43

3 Answers3

3

This is an extension of user3386109's answer for mapping an array of arbitrary dimension d with shape (n,...,n) into a vector of size size(d,n) only containing the elements whose indices satisfy X_1 <= X_2 <= ... <= X_d.

index

size

Community
  • 1
  • 1
letmaik
  • 3,348
  • 1
  • 36
  • 43
1

The 3D version of the equation is 

index := (z * (z+1) * (z+2)) / 6 + (y * (y+1))/2 + x
user3386109
  • 34,287
  • 7
  • 49
  • 68
  • Great, thanks! Can you explain shortly how you derived the 6? It looks like it is easily extendable to arbitrary dimensions. – letmaik Mar 13 '15 at 08:03
  • @neo It does appear that you could extend this to additional dimensions. However, I have not been able to prove it for 4D. The formula for 3D can be derived from the sum-of-squares, which wikipedia calls the [Square pyramidal numbers](http://en.wikipedia.org/wiki/Square_pyramidal_number), and that's where the 6 comes from. – user3386109 Mar 13 '15 at 18:54
  • To finish the 3D case, can you give the length of the resulting vector when the input array is `(n,n,n)`? – letmaik Mar 13 '15 at 20:47
  • @neo I believe that would be the index of coordinate `(n,0,0)`, i.e. the index of the first coordinate that is *not* in the array. Hence `size := (n * (n+1) * (n+2)) / 6` – user3386109 Mar 13 '15 at 20:53
  • Thanks! I just figured out the 4D case: `index := (l * (l+1) * (l+2) * (l+3) )/24 + (k * (k+1) * (k+2))/6 + (j * (j+1))/2 + i` for `M[i,j,k,l]`, and the vector has size `n*(n+1)*(n+2)/6*(n+3)/4`. 24=6*4. – letmaik Mar 13 '15 at 20:59
  • @neo That seems reasonable, but I can neither confirm nor deny it at this time. May have more time next week to look at it :) – user3386109 Mar 13 '15 at 21:35
  • I figured out the scheme, see my answer. Thanks for leading me to the right path! :) – letmaik Mar 13 '15 at 21:40
0

In case someone interested, here is the code of @letmaik answer in python:

import math
from itertools import combinations_with_replacement

import numpy as np

ndim = 3  # The one you'd like
size = 4  # The size you'd like
array = np.ones([size for _ in range(ndim)]) * -1
indexes = combinations_with_replacement([n for n in range(size)], ndim)


def index(*args):
    acc = []
    for idx, val in enumerate(args):
        rx = np.prod([val + i for i in range(idx + 1)])
        acc.append(rx / math.factorial(idx + 1))
    return sum(acc)


for args in indexes:
    array[args] = index(*args)


print(array)

Although I must confess it could be improved as the order of the elements do not seem natural.

BorjaEst
  • 390
  • 2
  • 11