4

we have a line segment L defined by two points from polygon and a polygon P define by 4 or more points, I need an algorithm determine if L is inside P?

EDIT: The line segment must be completely inside the polygon, if only partly it will defined as outside.

for example look below picture:

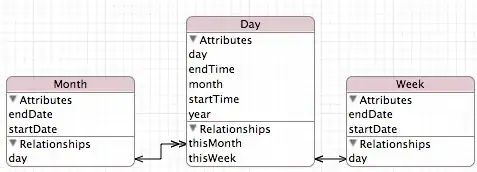
click to view image

few more examples:

click to view image

user3878881
  • 61
  • 3

2 Answers2

5

Step 1: Is L crossing any edge of P? If yes, L is not inside P. If no, see step 2

Step 2: Where is the middle M of L? If M is inside P, L is inside P.

Just in case: http://en.wikipedia.org/wiki/Point_in_polygon

Edit, more explanations: There are two cases :

  • L crosses at least one edge of P. Then L it at least partly inside P.
  • L does not cross any edge of P. Then L is either outside or inside. And as the entire L is outside or inside, it is sufficient to test the position of any point of L (except the two ends of L). And testing if a point is outside or inside a polygon is a classic problem (that have a dedicated wikipedia page).
Fumidu
  • 288
  • 4
  • 14
  • That's a really complicated step 2. – QuestionC Mar 17 '15 at 14:56
  • 1
    I erased my negative comment. Your algorithm is indeed correct and simple. Testing if a point is inside a polygon is quite simple. We consider an horizontal half line with the point as origin and we count the number of times the border of the polygon crosses the line. If it is an odd number, the point is inside. I delete my incomplete answer. I edited your answer to be able to undo my down vote. – chmike Mar 17 '15 at 15:16
  • @chmike Thank you. I also added more details. I should also add a picture to make the explanation easier to understand, but I don't really have time. – Fumidu Mar 17 '15 at 15:21
  • 1
    Actually your algorithm is not entirely correct. There are cases where _L_ does not intersect with any of the edges of _P_ and the centre _M_ is inside _P_ but _L_ is outside of _P_. That happens when _M_ lies on one or more edges of _P_. Which in turn happens either if that edge and _L_ are collinear or alternatively if _M_ is a vertex of _P_. – Dolma Oct 04 '18 at 12:53
  • @Dolma Indeed. There are some edge cases (pun intended) that need to be taken care of. But first, the problem needs to be refined: We need to decide wether _P_'s boundary is part of _P_, but the original question does not specify it. Anyway : with _M_ middle of _L_ (but let's define _L = AB_), if _M_ is on the border of _P_, then repeat reccursively the algorithm with _AM_ and _MB_ : _AB_ is inside _P_ only if _AM_ and _MB_ are inside _P_. – Fumidu Oct 05 '18 at 13:40
-2

If a line segment is completely inside a polygon, then there will be at least 1 polygon vertex on either sides of the line. See How to tell whether a point is to the right or left side of a line for finding which side a point is on.

UPDATE: However, the vice-versa may not be true. One should traverse all the polygon vertices in order starting from one end of the line segment. All vertices encountered in traversal from start to end of line segment should be on one side and the remaining should be on the other side.

The above will not be true if the line segment coincides with one of the edges of the polygon. In that case, there will be no vertex on one side of the line. However, in this case, the line is not lying completely inside the polygon either.

Community
  • 1
  • 1
sray
  • 584
  • 3
  • 8
  • 2
    This is completely wrong. What about 1->4 ? There are points on both sides, and the segment is not completely inside. You can also have points on both sides with a segment being completely outside. – ElderBug Mar 16 '15 at 14:21
  • Updated my answer to handle the reverse case, – sray Mar 16 '15 at 14:34
  • 2
    This is still wrong. You can have a segment inside that doesn't meet the requirement you mentioned. – ElderBug Mar 16 '15 at 14:49