I'm learning assembly on my own, I have a confusion that I would like to clear.
So from what I understand a x86 computer uses the same circuit for addition and subtraction. For subtraction a negative number is converted to its 2 complement and then the addition circuit could be used to carry out the subtraction. Eg: The equation 4 - 2 is converted to 4 + (-2)
So if subtraction can be done using the 2 complement then what is the purpose of the SUB Instruction?
In the 2's complement world, the negation of an integer can be obtained by taking the 1's complement (all bits inverted) and adding 1. For example, using 8-bit arithmetic:
A: 0x00000002 ; my number
~A: 0xFFFFFFFD ; 1's complement of my number
-A: 0xFFFFFFFE ; 2's complement of my number (negative A)
To subtract A-B, surely we can add the negative, A+(-B):
NOT B ; invert each bit in the 8-bit value, B
ADD B, 1 ; add 1, giving the 2's complement negated B
ADD A, B
And of course I had to modify B (negate it) before I could add it. What if I wanted B to stay intact?
PUSH B ; save B
NOT B ; invert each bit in the 8-bit value, B
INC A ; add 1, giving the 2's complement negated B
ADD A, B
POP B ; restore B
Or
NOT B ; invert each bit in the 8-bit value, B
INC A ; add 1, giving the 2's complement negated B
ADD A, B
NOT B ; restore B
So that works. But wouldn't it be easier to just have a SUB instruction?
SUB A, B
If you were writing assembly language to do a lot of arithmetic, which method would you prefer? And, in the first case I used an INC A instruction. I could get away without having INC and just use ADD A, 1. But an ADD A, 1, on many microprocessors, requires that I fetch more from the instruction memory to execute in order to obtain the immediate 1 value. Thus, an INC is provided since such an operation is so common.
When microprocessor designers determine what instruction set to have, they think about what sorts of operations would be most commonly used. Subtraction is pretty common, so a SUB instruction is quite handy to have. Therefore, it exists in just about any instruction set you'll find. There are other instructions in the instruction set whose reason for existence is much less obvious. The x86, for example, has the XLAT instruction, and all of the "string" instructions, LODS, STOS, etc. Why do they exist when I can do all that work with MOV and INC, etc? Because someone decided that these operations are common enough to merit having a single instruction.
So the purpose behind the SUB instruction, like many others implemented by the CPU, is to provide a faster (execution time) and simpler way to perform operations that are most commonly performed in software, balanced with the fact that there's a practical limit to how many instructions can be implemented.
Because it's one of the most common operations, having a dedicated instruction for it helps improving speed. Designers know how to make it fast and a separate negation isn't needed as you think
From the famous computer architecture books Computer Organization and Design, Fourth Edition: The Hardware/Software Interface by David A. Patterson and John L. Hennessy and Digital Design and Computer Architecture by David Money Harris, Sarah L. Harris we know that MIPS design principles are as below
Those are also correct in other architectures. In x86 and many other (mainly older) architectures some cannot be achieved because of backward compatibility, but the main points apply.
Because of the 1st and 3rd principles, we need to make the instruction set as compact as possible and don't create new instructions if we can do it using other instructions. However as per principles 2 and 4, we need to make the common operations as fast as possible.
In fact most instructions are redundant as we can have as a Turing complete instruction set with only one instruction. x86 itself is not an OISC architecture but it's still possible to do anything with just a single mov or add/sub because they're proved to be Turing-complete. There's even a compiler to compile valid C code into a program with only MOV (or only either of XOR, SUB, ADD, XADD, ADC, SBB, AND/OR, PUSH/POP, 1-bit shifts, or CMPXCHG/XCHG) named movfuscator
So with add or sub we can get shifts, bitwise operations and multiplication/division easily. However those basic operations may need extremely long series of instructions to simulate, and users won't be happy with that.
That's why manufacturers continuously add new instructions to the new microachitectures because newer demands will make things not common before come into use a lot. For example they decided to add SIMD instructions for vector and 3D operations when 3D applications was becoming a new trend, and matrix operations are also common. And then when increasing security requirements make encryption more common, AES instructions were introduced to boost cryptography applications. But that's not enough, as cryptography and many other applications use a lot of multiprecision arithmetics, Intel added MULX/ADOX/ADCX instructions to make those faster. And now you'll see instructions to accelerate AI operations begin to get into architectures
Back to the main question, subtraction is extremely common so that it's worth a separate instruction. Without it you'll have to negate one operand and then add, which cost at least twice the time and instruction space. sub a, b is better than neg b; add a, b.
However subtraction isn't necessarily slower because of the negation as you thought because designers use a clever trick to make adders do both add and sub in the same number of clocks by adding only a muxer and a NOT gate along with the new input Binvert in order to conditionally invert the second input as below
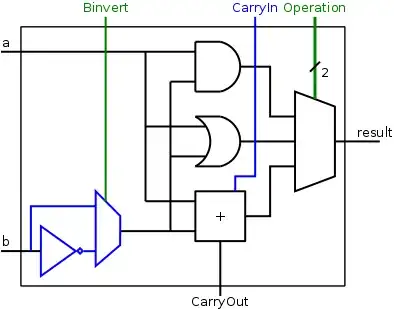
Computer Architecture - Full Adder
Basic it works by realizing that in two's complement -b = ~b + 1, so a - b = a + ~b + 1. That means we just need to set the carry in to 1 (or negate the carry in for borrow in) and invert the second input.
This type of ALU was also mentioned in the books I mentioned at the beginning. Unfortunately I can't quote it due to licensing problems, but I've found in another book from prof. Patterson and prof. Hennessy:
Computer Organization and Design RISC-V Edition: The Hardware Software Interface
As you can see, with another very simple modification they can now do 6 different operations with a single ALU: add, sub, slt, and, or, nor
CSE 675.02: Introduction to Computer Architecture
In fact designers are very smart at sharing components for saving space, for example they can produce an ALU that works for both ones' and two's complement, or an ALU that shares things with the FPU
You can find more information in ALU design courses, or on Google with the keywords Binvert/Bnegate
As others said, a SUB instruction is not strictly needed. For example, on the important PDP-8 computer from 1965 there is no subtraction instruction. Instead, you have to subtract the other way round. For example, to compute A - B you would do something like this:
/ ASSUMING THE ACCUMULATOR AC IS INITIALLY CLEAR
TAD B / ADD B TO AC (GIVING B)
CMA IAC / COMPLEMENT AND THEN INCREMENT AC (GIVING -B)
TAD A / ADD A TO AC (GIVING A - B)
Here TAD stands for “two's complement add,” CMA for “complement accumulator,” and IAC for “increment accumulator.”
But that said, you don't even need an ADD instruction. For example, the popular 6502 processor from 1975 famously lacks an ADD instruction, having only an ADC (add with carry) instruction. So if you want to do an addition, you first have to ensure the carry flag has been cleared. This is usually easy to achieve as many instructions clear the carry flag as a side effect. If that's not the case, you have to manually clear it with a CLC instruction.
Likewise, no subtraction instruction existed. You had to use the SBC (subtract with carry) instruction which required you to set the carry flag with a SEC instruction beforehand to do a normal subtraction.
