How do I iterate over Binary Tree?

Question

Right now I have

 private static void iterateall(BinaryTree foo) {
    if(foo!= null){
    System.out.println(foo.node);
    iterateall(foo.left);
    iterateall(foo.right);
   }
  }

Can you change it to Iteration instead of a recursion?

Answer 1

What you're looking for is a successor algorithm.

Here's how it can be defined:

• First rule: The first node in the tree is the leftmost node in the tree.
• Next rule: The successor of a node is:
  • Next-R rule: If it has a right subtree, the leftmost node in the right subtree.
  • Next-U rule: Otherwise, traverse up the tree
    • If you make a right turn (i.e. this node was a left child), then that parent node is the successor
    • If you make a left turn (i.e. this node was a right child), continue going up.
    • If you can't go up anymore, then there's no successor

As you can see, for this to work, you need a parent node pointer.

---

Example:

• First rule: The first node in the tree is the leftmost node in the tree: (1)
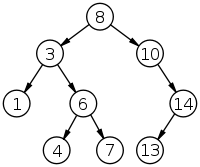
• Next-U rule: Since (1) has no right subtree, we go up to (3). This is a right turn, so (3) is next.
• Next-R rule: Since (3) has a right subtree, the leftmost node in that subtree is next: (4).
• Next-U rule: Since (4) has no right subtree, we go up to (6). This is a right turn, so next is (6).
• Next-R rule: Since (6) has a right subtree, the leftmost node in that subtree is next: (7).
• Next-U rule: Since (7) has no right subtree, we go up to (6). This is a left turn, so we continue going up to (3). This is a left turn, so we continue going up to (8). This is a right turn, so next is (8).
• Next-R rule: Since (8) has a right subtree, the leftmost node in that subtree is next: (10).
• Next-R rule: Since (10) has a right subtree, the leftmost node in that subtree is next: (13).
• Next-U rule: Since (13) has no right subtree, we go up to (14). This is a right turn, so next is (14).
• Next-U rule: Since (14) has no right subtree, we go up to (10). This is a left turn, so we continue going up to (8). This is a left turn, so we want to continue going up, but since (8) has no parent, we've reached the end. (14) has no successor.

---

Pseudocode

Node getLeftMost(Node n)
  WHILE (n.leftChild != NULL)
    n = n.leftChild
  RETURN n

Node getFirst(Tree t)
  IF (t.root == NULL) RETURN NULL
  ELSE
     RETURN getLeftMost(t.root);

Node getNext(Node n)
  IF (n.rightChild != NULL)
     RETURN getLeftMost(n.rightChild)
  ELSE
     WHILE (n.parent != NULL AND n == n.parent.rightChild)
        n = n.parent;
     RETURN n.parent;

PROCEDURE iterateOver(Tree t)
  Node n = getFirst(t);
  WHILE n != NULL
     visit(n)
     n = getNext(n)

---

Java code

Here's a simple implementation of the above algorithm:

public class SuccessorIteration {
    static class Node {
        final Node left;
        final Node right;
        final int key;
        Node parent;
        Node(int key, Node left, Node right) {
            this.key = key;
            this.left = left;
            this.right = right;
            if (left != null) left.parent = this;
            if (right != null) right.parent = this;
        }
        Node getLeftMost() {
            Node n = this;
            while (n.left != null) {
                n = n.left;
            }
            return n;
        }
        Node getNext() {
            if (right != null) {
                return right.getLeftMost();
            } else {
                Node n = this;
                while (n.parent != null && n == n.parent.right) {
                    n = n.parent;
                }
                return n.parent;
            }
        }
    }
}

Then you can have a test harness like this:

static Node C(int key, Node left, Node right) {
    return new Node(key, left, right);
}
static Node X(int key)             { return C(key, null, null);  }
static Node L(int key, Node left)  { return C(key, left, null);  }
static Node R(int key, Node right) { return C(key, null, right); }
public static void main(String[] args) {
    Node n =
        C(8,
            C(3,
                X(1),
                C(6,
                    X(4),
                    X(7)
                )
            ),
            R(10,
                L(14,
                    X(13)
                )
            )
        );
    Node current = n.getLeftMost();
    while (current != null) {
        System.out.print(current.key + " ");
        current = current.getNext();
    }
}

This prints:

1 3 4 6 7 8 10 13 14 

See also

• Complete Java listing and output on ideone.com

Answer 2

Can you change it to Iteration instead of a recursion?

You can, using an explicit stack. Pseudocode:

private static void iterateall(BinaryTree foo) {
    Stack<BinaryTree> nodes = new Stack<BinaryTree>();
    nodes.push(foo);
    while (!nodes.isEmpty()) {
        BinaryTree node = nodes.pop();
        if (node == null)
            continue;
        System.out.println(node.node);
        nodes.push(node.right);
        nodes.push(node.left);
    }
}

But this isn’t really superior to the recursive code (except for the missing base condition in your code).

Answer 3

Sure, you have two general algorithms, depth first search and breadth first search.

If order of traversal is not important to you, go for breadth first, it's easier to implement for iteration. You're algorithm should look something like this.

LinkedList queue = new LinkedList();

queue.add(root);

while (!queue.isEmpty()){
    Object element = queue.remove();

    queue.add(element.left);
    queue.add(element.right);

    // Do your processing with element;
}

Answer 4

As with every recursion, you can use additional data structure - i.e. the stack. A sketch of the solution:

private static void visitall(BinaryTree foo) {
  Stack<BinaryTree> iterationStack = new Stack<BinaryTree>();
  iterationStack.push(foo);

  while (!iterationStack.isEmpty()) {
      BinaryTree current = iterationStack.pop();
      System.out.println(current.node);
      current.push(current.right);        // NOTE! The right one comes first
      current.push(current.left);
   }

}

Answer 5

I had a tree (not binary) and eventually solved it with this very simple algorithm. The other solutions used left and right that were not relevant or even implemented in the examples.

My structure was: nodes with each parent containing list of children, and each child containing a pointer back to the parent. Pretty common...

After a bunch of refactoring, I came up with the following example using Kotlin. It should be trivial to convert to your language of choice.

Helper Functions

First, the node must provide 2 simple functions. This will vary depending on your Node class' implementation:

leftMost - This is the first child node. If that node has children, it's first child, etc. If no children, return this.

fun leftMost(): Node {
        if (children.isEmpty()) {
            return this
        }
        var n = this
        while (n.children.isNotEmpty()) {
            n = n.children[0]
        }
        return n
}

nextSibling - The next sibling of this node, or NULL

fun nextSibling(): Node? {
    if (parent == null) return null
    val siblingIndex = parent.children.indexOf(this) + 1
    return if (siblingIndex < parent.children.size) {
        parent.children[siblingIndex]
    } else {
        null
    }
}

The Iteration

The iteration starts with the leftMost of the root.

Then inspect the next sibling.

• If NOT NULL the sibling's leftMostChild
• If NULL, the parent, and if the parent is NULL, we are done.

That's it.

Here is a Kotlin iterator function.

fun iterator(): Iterator<Node> {
    var next: Node? = this.leftMost()

    return object : Iterator<Node> {

        override fun hasNext(): Boolean {
            return next != null
        }

        override fun next(): Node {
            val ret = next ?: throw NoSuchElementException()
            next = ret.nextSibling()?.leftMost() ?: ret.parent
            return ret
        }
    }
}

Here is the same next() function, but without the Kotlin shorthand for dealing with NULL values, for those that are not hip to the syntax.

fun next(): Node {
    val ret = next
    if (ret == null) throw NoSuchElementException()
    val nextSibling = ret.nextSibling()
    if (nextSibling != null) {
        next = nextSibling.leftMost()
    }
    else {
        next = ret.parent
    }
    return ret
}

Answer 6

Yes, you can change it to iteration instead of a recursion, but then it gets much more complicated, since you need to have some way to remember where to go back from the current node. In the recursive case, the Java call stack handles that, but in an iterative solution you need to build your own stack, or perhaps store back pointers in the nodes.